Functional Causal Discovery - [1] ANM
Summary: 비선형성으로 identifiablity를 찾은 방법
이번 글에서는 Causal Learning의 또다른 주축인 Causal Discovery, 그리고 이를 위한 방법 중 하나인 ANM에 대한 논문 (Hoyer at al., Nonlinear causal discovery with additive noise models (2008)) 을 소개하고자 합니다. Causal Discovery는 데이터로부터 (추가적인 randomized experiments없이) 인과관계를 밝혀내는 방법입니다. 인과관계를 밝히기란 굉장히 어려울 것 같은데, 이 논문에서는 다양한 가정을 두고 변수 간 인과관계를 찾아낼 수 있는 방법을 소개합니다. 그 방법으로 비선형인 인과관계 메커니즘과 additive 노이즈 항을 두는 단순한 방법을 제안합니다.
Methods
Causal Discovery, ANM의 목표는 주어진 데이터로부터 생성 메커니즘 혹은 생성 그래프를 추론하는 것입니다.
기본적으로 다음과 같은 가정을 두고 모델을 만듭니다. 관측된 데이터를 DAG로 표현했을 때, i번째 노드에 해당하는 변수의 데이터는 그것의 parents 노드들의 함수로써 얻어질 수 있다고 가정합니다. 여기서 노이즈 변수는 독립이며 additive로 더해집니다. \(x_i:=f_i(\mathbf{x}_{pa(i)}+n_i)\)
이제 Idenfiability를 확인할 것입니다.
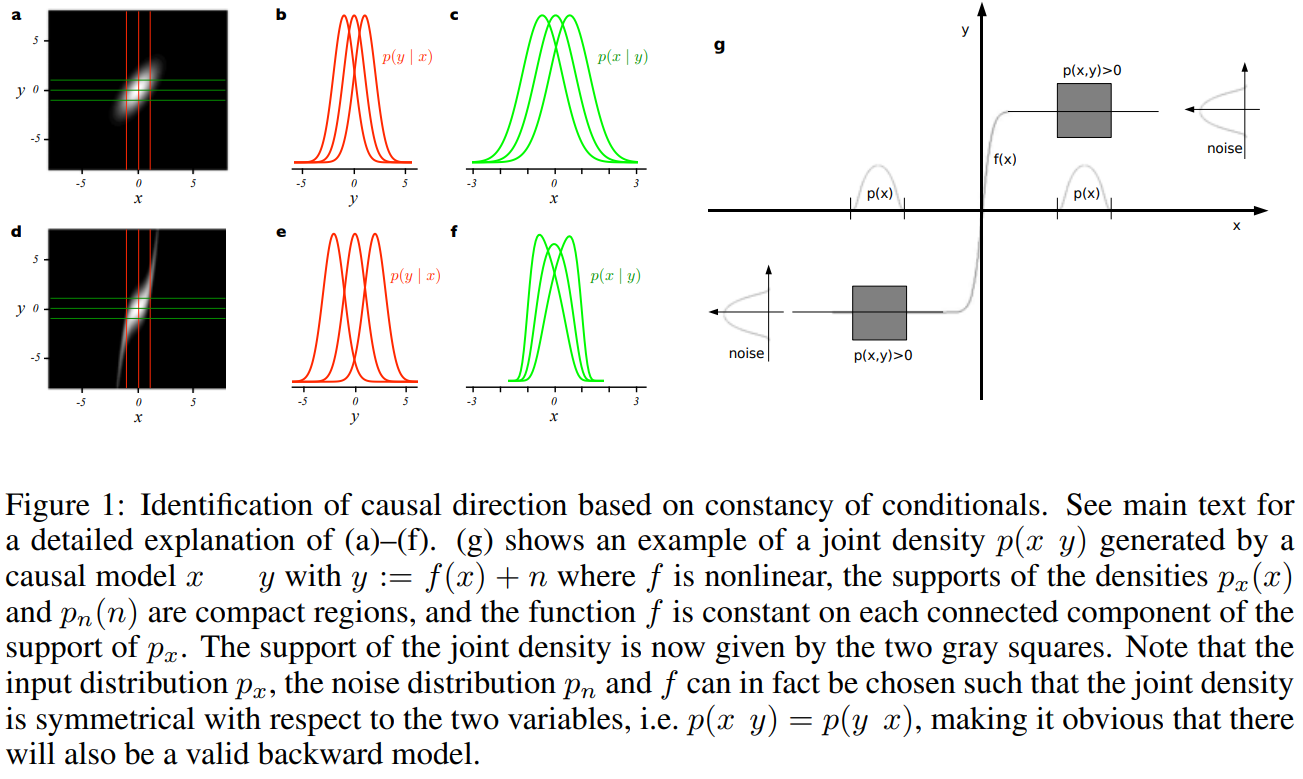
위의 그림을 보면, 재밌는 사실을 (경험적으로) 발견할 수 있습니다. 첫번째 행에서 \(f_i\)가 선형 함수(linear function)이면 Gaussian이라 \(p(y|x),p(x|y)\) 를 구별하지 못하고, ‘대칭성’ 때문에 non-identifiable함을 볼 수 있습니다. 즉, \(x\xrightarrow{}{}y\)인지 \(y\xrightarrow{}{}x\)인지 어렵습니다. 반대로 두번째 줄에서는 \(f_i\)가 비선형 함수 관계를 가정하는데, 이는 조건부 분포 2개를 구별할 수 있게 되면서 이 비대칭성 때문에 identifiable하게 됩니다.
Theorem 1: \(f,p_x,p_n\)을 일반적으로(generic하게) 선택해도 identifiable합니다.
가정: 모든 probability density는 positive이고 모든 함수들은 3번 미분가능하다.
의미: \(xi\)에 대한 미방이 3차원의 해를 가지고 forward가 inverted될 수 있습니다. 즉, \(p_x,noise \sim \mathcal{N}\) 이면 backward가 존재한다는 것은 즉, \(f\)가 선형이라는 의미입니다.
증명
Corollary: nonlinear이지만 backward model이 있는 경우(non-idenfiable)도 있다.
증명
이 가정들과 모델을 실제 분석 시 적용해봅시다. 먼저, 이변량일 때 분석과정은 다음과 같습니다.
- \(X,Y\) 간 독립성 테스트를 수행합니다.
- 모델 \(y:=f(x)+n\)이 데이터에 consistent한지 검정합니다.
- \(y\)에 대한 \(x\)의 비선형회귀모델 적합: 이 논문에서는 GPR(Gaussian Process Regression)을 사용합니다.
- 잔차 \(n=y-f(x)\)의 독립성 검정을 수행합니다.
- 독립이면, 현재 모델을 채택합니다.
- \(x:=g(y)+n\)이 데이터에 fit한지 테스트 (위 2.와 같은 방법으로)합니다.
- 결과는 다음과 같이 해석합니다.
- \(X,Y\)가 독립이면, causality는 없다고 결론을 내립니다.
- 독립이 아니면,
- 두 모델 다 맞을 경우 둘 중 하나 선택합니다.
- 둘 다 아니면, 인과 메커니즘이 복잡해서 이 모델로 적합할 수 없는 걸로 결론 내립니다.
다변량일 경우, 분석은 변수가 \(N\)개인 경우 DAG를 가정하여 Y는 \(x_i\), X는 \(x_i\)의 parents라고 하고 똑같이 하면 됩니다.
ANM 모델이 커버하지 못하는 단점은, 첫째, 변수 수 적을 때 (\(N\le 7\)) 일 때만 가능합니다. 둘째, multiple hypothesis testing 문제가 발생합니다. 셋째, subgraph가 존재하면 모든 DAG가 다 accept 해버리게 됩니다.
Experiments
Simulation data
model: \(y=x+bx^3+n$, $x,n \sim \mathcal{N}\)
\(q\): power → non-Gaussianity parameter
\(b\): nonlinearity parameter
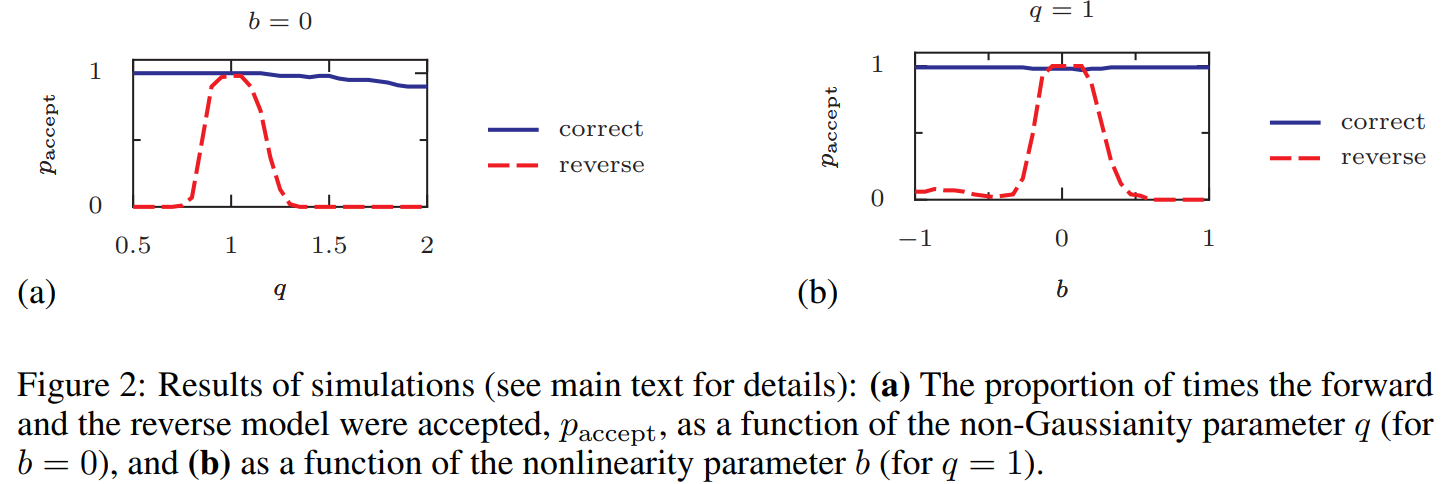
위의 그래프는 \(b\)와 \(q\) 값에 따른 accept할 확률을 의미합니다.
\(b=0, q=1\) 근처에서 backward 모델도 accept할 확률이 커지므로 이 모델은 non-identifiable합니다.
Real-world data: Old Faithful
간헐천 데이터로, 현재와 다음 폭발 간의 시간 간격(interval)은 현재 폭발의 기간(duration)에 대한 관계를 보여줍니다. 우리는 duration이 interval에 영향을 주는 원인인지 알고 싶습니다.
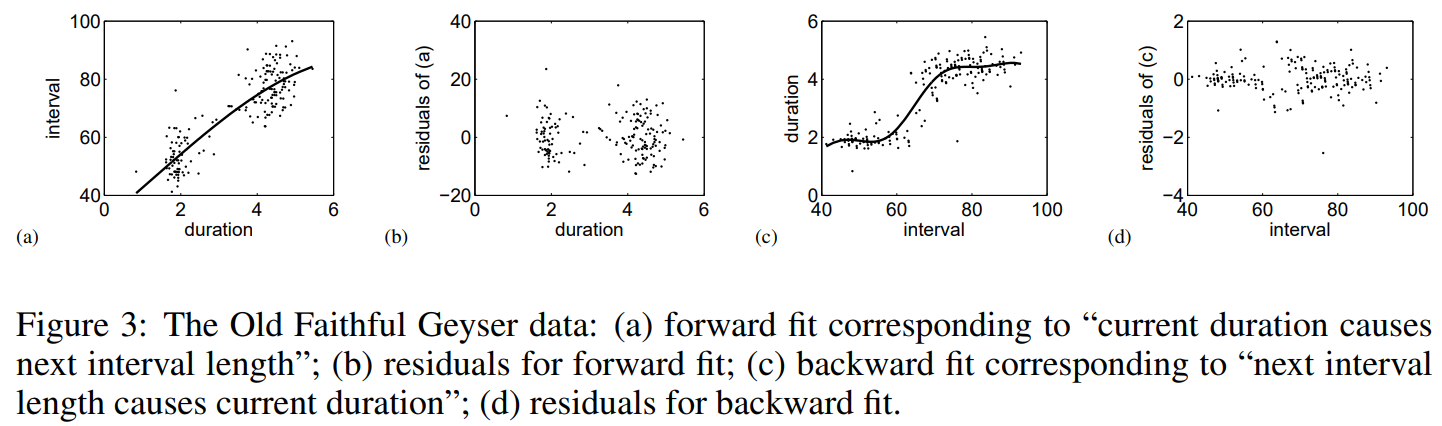
위의 스캐터 플랏은 (a) 모델 적합 결과, (b) 적합된 모델의 잔차 플랏, (c) backward 모델 적합 결과 (current -> next), (d) 적합된 backward 모델의 잔차 플랏을 의미합니다.
논문 본문에서는 이 결과를 잔차들의 독립성 검정에 대한 p-value로 설명하고 있습니다(추측컨대 ㅠㅠ). forward model은 p-value가 0.5이고, 매우 작고, backward model의 p-value는 매우 작게 나타났습니다. 따라서 우리는 forward model을 accept하여, duration이 interval의 cause라고 결론내릴 수 있습니다.
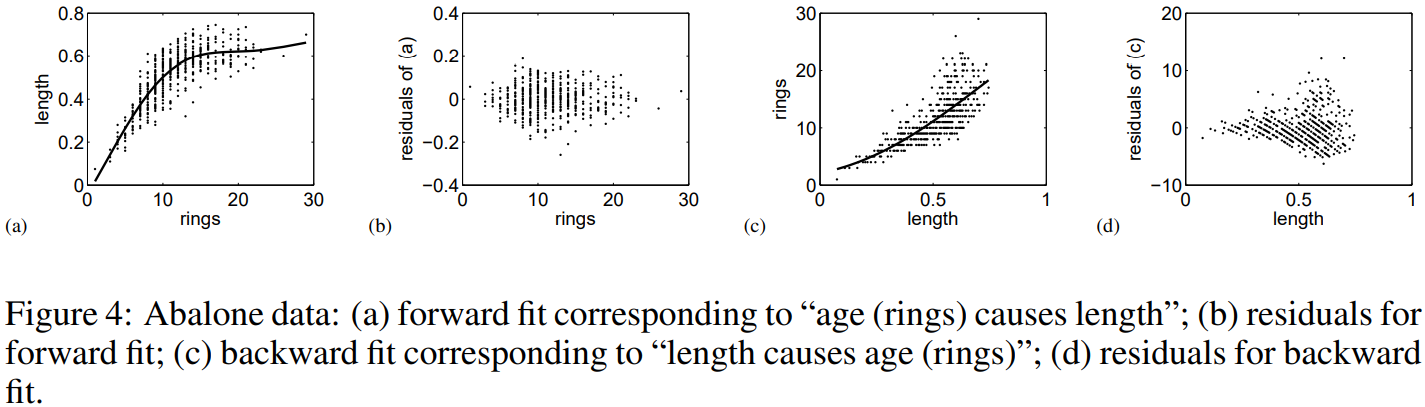
Real-world data: Abalone data
Abalone 데이터는 전복(조개류)의 껍질에 있는 ring의 숫자, 나이, 껍질의 길이를 측정하는 것입니다. 우리는 나이가 길이에 영향을 미치는지 알고 싶습니다.
이 또한 위의 플랏 순서이며, p-value를 통해 결과를 살펴보면, 나이가 길이에 영향을 주고, 그 반대 원인-효과 모델은 기각됩니다.
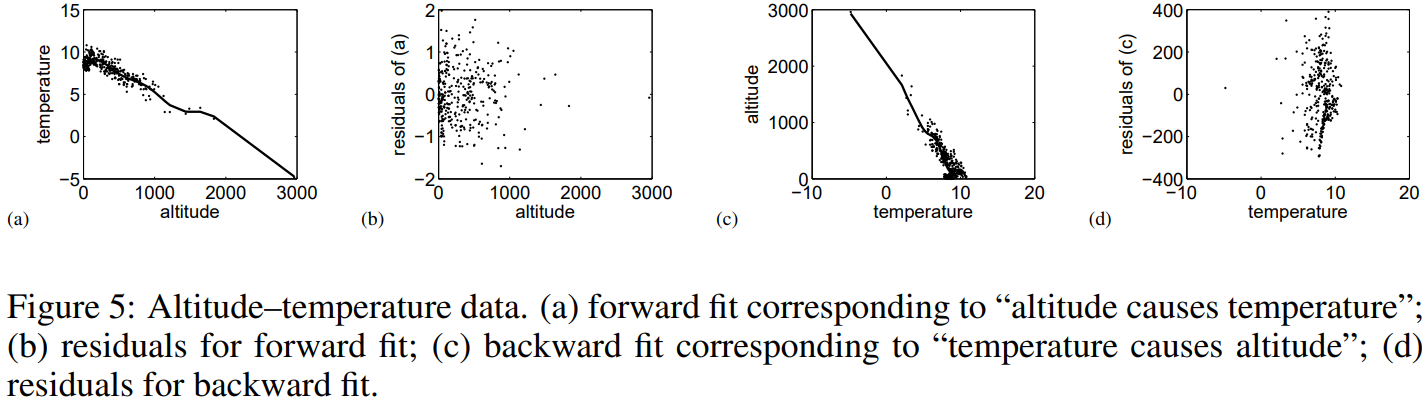
Real-world data: Altitude-temperature data
유명한 예제인 고도와 기온에 대한 데이터입니다. 당연하게도 고도가 기온의 원인일텐데, 실제로 분석 결과도 p-value를 통해 이를 입증하고 있습니다.
Conclusion
충분히 간단하고 일반적으로 사용되기 쉬울 수 있다는 ANM에 대해 살펴보았습니다. nonlinear인 cause와 effect의 관계를 설명할 수 있고, (independent) Gaussian additive noise로 단순성을 더했습니다.
다음 포스팅에서는 다른 causal discovery 모델에 대해 다루겠습니다.
References
Hoyer, P., Janzing, D., Mooij, J. M., Peters, J., & Schölkopf, B. (2008). Nonlinear causal discovery with additive noise models. Advances in neural information processing systems, 21, 689-696.