ECI-1. Statistical and Causal Methods

1. Statistical and Causal Methods

Elements of Causal Inference: Foundations and Learning Algorithms 라는 책을 공부하고 (가능한 한) 제 표현으로 정리한 글입니다.

먼저 이 책은 Causal Inference 분야의 대가인 Jonas Peters, Dominik Janzing, and Bernhard Schölkopf 교수님께서 쓰신 책입니다. 인과 추론을 통한 원인과 결과에 대한 이론과, 머신러닝을 연결하는 방법에 대해 다루고 있습니다. Causal Learning 분야는 크게 원인과 결과가 무엇인지 밝혀내는 Causal Discovery와 원인과 결과가 주어졌을 때 결과를 추론하는 인과 추론(Causal Inference) 분야로 나뉩니다.

Causal Learning은 어렵습니다. 기본적으로 무엇이 원인이고 결과인지를 밝혀내는 것이 어려울 뿐만 아니라, 결과에 대한 원인의 영향력을 정확하게 측정하기 어렵기 때문입니다. 이는 잘 통제된 ‘Randomized Experiments’가 필요하기 때문입니다. 이는 앞선 글인 Causal Discovery - [0] Overview에서 간단하게 설명드렸습니다.

책에서 서술한 순서와 다르게, 여기서는 우리에게 친숙한 예제들을 먼저 설명하고, 이에 포함된 개념과 그 중요성에 대해서 소개하고자 합니다.

Pattern Recognition 예제 1: optical character recognition

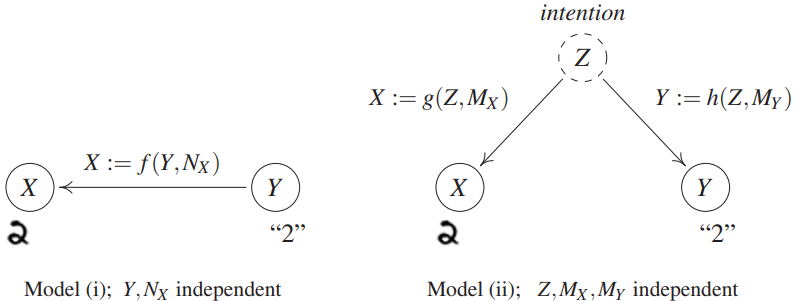
손으로 쓴 숫자 글씨(handwritten digits)로부터 해당 숫자가 무슨 숫자인지 예측하는 문제를 푼다고 생각해봅시다. 대표적으로 MNIST 이미지 데이터셋으로부터 숫자 클래스를 분류하는 예시 문제가 있습니다. 아래 그림과 같이 크게 두 가지 방식의 모델이 있습니다. 결론을 스포해보자면, 이 둘은 같은 통계적 모델을 말하지만 서로 다른 Causal Structure를 가집니다.

왼쪽 그림의 경우, 글씨를 쓴 사람($f$)이 ‘2’($Y$)라는 정해진 숫자를 보고 이를 글씨로 쓰는($X$) 가정(모델)을 그래프로 표현한 것입니다. 오른쪽 그림은 글씨를 쓴 사람이 어떤 의도(intention)을 가지고 무슨 숫자를 쓸지 결정하고, 이미지를 그리는 모델을 나타냅니다. 이 사람은 가끔 악필로 쓰게 될 때가 있어 noise($N_X,M_X$)도 있습니다. 이러한 여러 글씨 이미지(X)와 이에 해당하는 클래스(Y)에 대한 ‘관측 데이터(observational distribution)’로부터 잘 예측하는 것이 목표입니다.

여기서 Intervention(개입)의 개념을 간단히 설명드리고자 합니다. Intervention은 특정 변수를 조작하거나, 새롭게 생성하는 것을 의미합니다. 이 예시에서는 글씨 이미지를 다른 이미지로 바꾼다거나, 그리기로 정했던 숫자 ‘2’를 다른 숫자로 바꾸는 것을 의미합니다.

왼쪽 그림 모델의 경우, 누가 임의로 숫자 그림을 다른 그림으로 바꾸었다고 생각해봅시다. 그렇다면 숫자 2 (Y)도 바뀔까요? 그렇지 않을 것입니다. 이미 정해졌던 숫자를 보고, 그림을 그렸었기 때문에 그림을 바꾼다고 해당 숫자가 바뀌지는 않을 것입니다. 즉, 효과(effect)인 X를 변경해도 원인(cause)인 Y가 변하지는 않습니다. 반면에 숫자 Y를 바꾸는 것은 숫자를 쓰는 사람이 볼 때 다른 숫자로 그림을 그릴 것이므로 생성될 숫자 이미지에 영향을 줄 것입니다. Y를 변경하면 X에 영향을 미칩니다. 즉, 이 화살표로써 직접적인 인과관계(direct causation)을 나타냅니다. 수식적으로, X:=f(Y,N_X)로 표현합니다. 즉, X는 Y의 함수입니다.

오른쪽 그림의 경우, 글씨 그림 X을 누가 임의로 바꾸었다고 해봅시다. 이때도 숫자 Y가 바뀌지 않습니다. 그렇다면 숫자 Y를 바꾼다면 어떻게 될까요? 작성자의 의도가 담긴 Y를 바꾼다면 왼쪽 모델과는 달리 X에 영향을 주지 않습니다. 미리 정해졌던 Y를 바꾸어도 그리고자 한 의도(Z)는 바뀌지 않았기 때문입니다.

위처럼 X,Y에 대한 같은 관측 분포(observational distribution)을 가지면서도 다른 interventional 분포을 가질 수 있습니다. 이는 확률적 접근에서는 보기 어려우며 $P_{X,Y}$에 대한 구조적 지식(structural knowledge)이 필요합니다. X, Y 변수에 해당하는 ‘데이터가 어떻게 생성되는지’를 알아야 합니다. 이는 SCMs(structural causal models)의 예이며, 모든 관측치에 대한 결합 분포를 포함할 뿐 아니라 그래프 내 변수 간 방향성, 즉 구조적 지식이 추가적으로 필요합니다.

그리고 X와 Y의 그래프 구조에 따라 달라지는 intervention의 효과는 Reichenbach’s common cause principle로 설명할 수 있습니다. X와 Y 간 Z라는 공통의 원인(common cause)가 조건(condition)으로 있다면, X와 Y는 독립이 됩니다. 즉, 그림(X)과 숫자 레이블(Y)에는 더이상 글씨 작성자의 의도(Z)가 포함되지 않습니다. 이는 추후 다시 다루고자 합니다.

참고: 인과관계는 시간 개념이 꼭 있어야 한다? 그렇지 않습니다. 모두 하나의 동적 프로세스로 설명할 수 있습니다. 다만, 아주 엄격하고자 한다면 잘 정의된 time instance와 함께 physical model을 사용해야 할 것입니다.

Gene Perturbation 예제 2

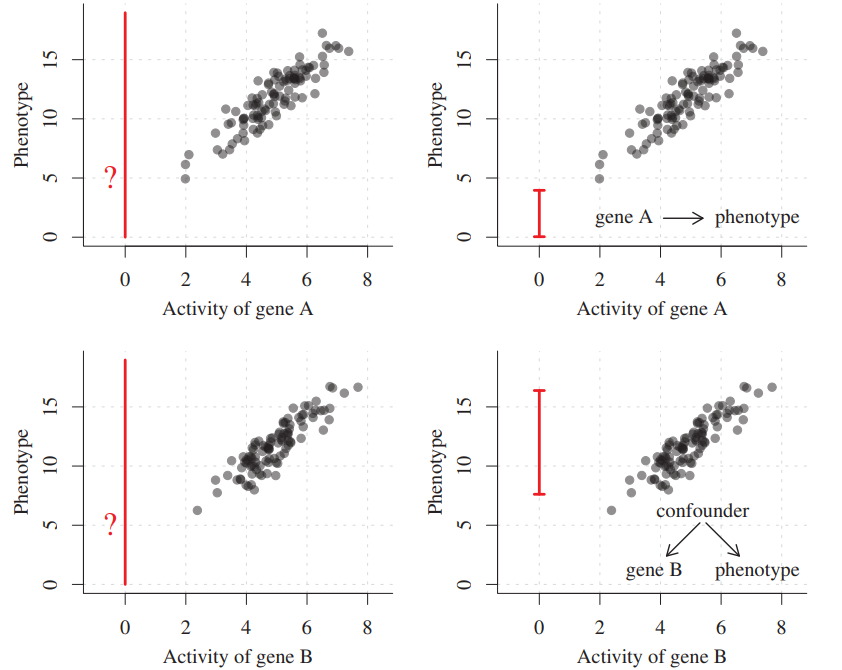
개입(intervention) 하에서 어떤 변수의 결과를 예측하고자 하면 어떨까요? Genetics에서의 예시를 생각해봅시다. 두 개의 유전자의 activity 데이터와 그에 해당하는 phenotype 측정값이 있습니다.

왼쪽은 일반 모델 오른쪽은 causal 모델

각 변수들 간 모두 강한 양의 상관관계가 있는 것으로 보입니다. 이는 일반적인 머신러닝에서 유전자 A와 B의 활성화 정도가 6 근처이면 표현형 값이 12 근처인 것으로 예측됩니다. 당연해보이죠?

여기서 유전자 A를 삭제한 후, 이 활성화값을 0.6으로 세팅한다면 표현형 값은 얼마일까요? 일반적인 머신러닝.. 선형회귀에서는 크게 어렵지 않게 (explo..) 예측할 수 있을 테지만, 인과 구조에 대한 지식이 있다면 다른 답을 낼 수도 있습니다.

유전자 A가 원인이고, 표현형이 결과라면, intervention 후에 표현형 측정값이 달라지겠죠 (오른쪽 상단 그림). 위에서 언급했듯, 선형회귀에서도 빨간색 선 안에서 예상대로 예측할겁니다.

만약 유전자 B와 표현형에 어떤 공통 원인(confounder)이 있다면 어떨까요? 그렇다면, 유전자 B가 바뀌어도 표현형에는 아무런 영향을 주지 않을 겁니다. 즉, 원래 표현형 측정값의 분포 내에서 예측이 되겠습니다 (오른쪽 하단 그림).

즉, 일반적인 선형회귀, 혹은 머신러닝 (심지어 popular한 딥러닝까지도!)은 이런 상관관계를 고려하여 예측하지만(Attention mechanism만 봐도..), 여기서는 인과 구조까지 고려하여 더 정확하게 예측할 수 있습니다.

Causal Modeling and Learning

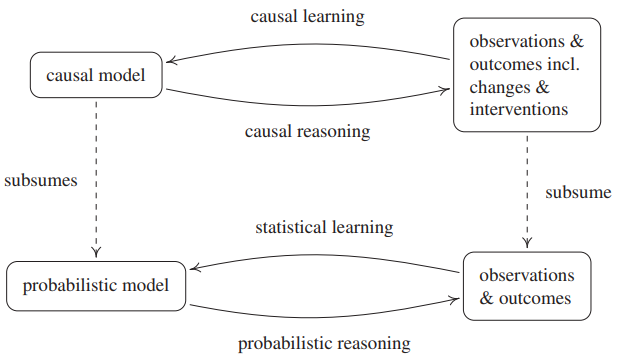
Causal Learning, Causal Reasoning, Statistical Learning, 그리고 probabilistic reasoning은 아래 그림과 같은 관계를 가집니다.

Figure 1.1: causal and probabilistic inference(learning+reasoning)

Causal Reasoning은 causal model로부터 결론을 도출하는 과정을 말합니다. probabilistic reasoning이 확률론으로부터 랜덤 실험의 결과를 추론한다면, causal reasoning은 확률 만이 아닌, 인과적 구조에 대한 정보를 더 가지고 있으므로 intervention의 효과 등을 알 수 있어 더 강력합니다.

Causal Learning은 관측치와 intervention으로부터 causal model를 추정하는 전반적인 문제들을 일컫습니다. statistical learning이 관측치들로부터 probabilistic model을 추론하는 inverse problem을 의미하는 것처럼, 관측치와 randomized trials와 같은 intervention으로부터, causal structure(인과적 구조, 그래프 구조라고 생각하시면 됩니다)를 찾아내는 것을 structure learning 혹은 causal discovery라 합니다. 이 자체는 어려운 문제인데, causal structure는 확률분포 P를 안다고 해서 알 수 있는 문제가 아니며, structure identifiability를 만족해야 하고, richer function class를 고려해야 할 수 있습니다. 이들은 이 책에서 나중에 나올 추가적인 가정들이 필요하며, 이 자체로는 ill-posed problem입니다.

Reichenbach’s common cause principle

이 문제를 풀기 위해선 causal model과 statistical model이 어떻게 연결되는지 알아야 합니다. 우리 모두 잘 알고 있는 말인, “correlation does not imply causation!”는 이번 글에서 살펴본 용어들로 표현하면 “statistical properties alone do not determine causal structure”를 말합니다. 즉, 통계적 종속성(dependency)으로부터 인과관계가 있다고 보기 어렵습니다.

여기서 아주 중요한 원칙인 “Reichenbach’s common cause principle”가 나옵니다.

Principle 1.1 (Reichenbach’s common cause principle) 두 개의 랜덤변수 X, Y가 통계적으로 독립이 아니면, 세번째 변수 Z가 존재하여, 인과적으로 두 변수에 영향을 준다는 것을 나타낸다. (특별한 경우, Z는 X 혹은 Y와 일치할 수도 있다.) 또한, 변수 Z가 given 되면, Z는 X와 Y를 서로 차단하게 되어 독립이 된다.

위 원칙은 통계적 종속성과 관련된 내용입니다. 물론, 종속성은 원칙 1.1 이외에도 다른 이유로도 발생할 수 있습니다. 1) 관측된 랜덤변수는 다른 변수에 대한 조건부가 되어 종속성이 나타납니다. 나중에 살펴보겠지만 selection bias와도 관련이 있습니다. 2) 랜덤변수가 종속일 때만 나타납니다. 예를 들어, 여러 쌍의 랜덤 변수들이 multiple testing correction 없이 단순하게 검색된다면, type1 error가 크게 나타납니다. 이건 confounder 등의 여러 causal 구조를 가정하지 않고 단순히 testing을 했기 때문입니다. 이 또한 뒤에서 다시 살펴보겠지요. 3) 두 확률 변수가 모두 시간에 대해 종속성을 가지고, (간단한) 물리적 법칙을 따를 경우, 종속성이 나타납니다. 이 경우, 변수가 서로 종속된 것이 아니라, i.i.d. 가정이 파괴되기 때문에 일반적인 independence test를 적용할 수 없어 종속이라고 밖에 할 수 없는 것입니다. 특히, 이는 요즘 많이 연구되고 있기도 한 ‘spurious correlations’ (가짜 상관관계) 를 보일 수 있기 때문에 항상 의심해보아야 합니다.

아래 그림은 Principle 1.1은 통계적 특성과 인과 구조 사이를 연결하는 것을 설명합니다. 두 관측치 X와 Y 간 통계적 종속성은 왼쪽 그림의 Z (Confounder)에 의해 발생합니다. 여기서 Z는 X 또는 Y와 일치할 수 있어 중간 그림과 오른쪽 그림처럼 나타날 수도 있습니다. 또한, X와 Y가 Z를 조건부로 가지게 되면, 통계적으로 독립이 됩니다.

Statistical and Causal Methods

다시 돌아와서.. 이러한 ‘영향’ 등을 고려한 causal model에서 probabilistic model과 공통점과 차이점에 대해서 소개합니다. causal model은 intervention의 존재로 인해 일반적인 확률 모델과 다릅니다. 그럼에도 불구하고, 기존의 Statistical Learning의 중요도는 여전히 유효합니다. Causal Learning도 어떤 (유한한) 데이터를 통해 인과 관계에 대하여 확률적으로 추론하고자 합니다. 따라서, statistical estimation에서 다루는 random variables 간 (joint) distribution에 대한 가정과, finite samples에 대한 여러 이론들이 여전히 causal learning 분야에서도 고려되야 할 대상이 됩니다.

Probability Theory and Statistics

Statistical learning의 근간인 확률론과 통계학은 수학적 구조를 정의하고 random experiments의 결과를 추론할 수 있어, causal inference에서 중요한 기초입니다. 그 중에서 언급할만한 것은 inverse problem입니다. inverse problem은 우리가 관찰할 수 없는 것(unknown distribution)의 속성을 추정하기 위해 연산(샘플링 등) 등을 통해 얻은 관찰값으로 추론하는 것을 말합니다. 예로, 우리가 unknown distribution으로부터 data를 sampling하여 classifier 등의 예측자를 추정하는 문제를 말합니다. 그외 i.i.d. 등은 이후에 관련 causal inference 이론과 함께 설명하고자 합니다.

Learning Theory

(Statistial) learning theory는 데이터에 기반에 예측 함수를 찾는 문제를 이론적(통계학, 함수해석학 등)으로 다루는 분야입니다.

Statistical & causal model에서 function class restriction의 중요성

위에 언급된 예시에서 다시 시작해서, 데이터로부터 얻은 empirical distribution으로부터 empirical estimates(e.g. classifier)를 추론한다면, 이는 ill-posed problem이라 합니다. unseen input에 대한 estimates(e.g. conditional expectation)가 정의되지 않기 때문입니다.

statistical learning에서는 얼마나 많은 관측값이 있든 상관없이, empirical 분포는 대부분 실제 분포에 완벽하게 근사하지 않으며 이 근사치의 작은 오차는 추정치에서의 큰 오차로 이어질 수 있는 것을 말합니다. 즉, 이는 우리가 empirical estimates $f^n$을 선택하는 function class에 대한 추가 가정 없이는 optimal quantities $f$에 근사한다고 보장 할 수 없음을 의미합니다.

Statistical learning theory에서 이러한 가정들은 용량(capacity) measure 측면에서 formalize 할 수 있습니다. 우리는 보통 데이터 셋에 적합할 수 있을 정도의 적절히 풍부한 function class로 모델링을 할텐데요. 여기서 함수 클래스가 작은 capacity를 갖도록 선험적으로 제한되는 경우, 해당 클래스의 함수를 사용하여 설명할 수 있는 데이터 셋은 보통 적습니다. 그래도 이 데이터를 어느정도 설명할 수 있다고 하면 이로부터 우리가 어떤 규칙성을 발견했다고 봅니다. 그러면 같은 분포로부터 샘플링된 future data에 대한 solution의 정확도에 확률적인 보장을 줄 수 있게 됩니다.

여전한 causal model의 어려움..

Statistical learning의 complexity는 주로 유한한 empirical 데이터로 inverse problem을 해결하려 한다는데에서 발생합니다. 그러나 causal model은 ill-posed problem인데, statistical learning에서의 statistical ill-posed-ness 뿐만 아니라, 관찰 분포를 다 잘 알더라도, causal structure까지 알아야 하므로 이 방면에서의 ill-posed-ness까지 있다고 볼 수 있습니다.

Distribution Shift 문제와 인과 모델의 관계

최근 머신러닝의 성공은 종종 놀라운 결과를 보여주고 있습니다. 그러나, 기존 머신러닝의 세팅에서 underlying 분포가 intervention이나 다른 변화에 의해 training과 test 간에 다르지 않아야 합니다. 그리고 이 분포 변화는 intervention 등으로 인해 아주 쉽게 나타날 수 있습니다. 즉, training set에서의 규칙성을 확률분포로 찾아 분포가 같은 test set에서 설명하는 것들은 (이 책의 주장으로는..) 분포 변화 등을 제대로 설명할 수 없습니다.

이번 챕터에서는 확률 모델들과 인과 모델이 다루는 것들의 주요한 차이점들을 간단히 살펴보았고, 다음 챕터부터는 각각을 하나하나 살펴보고, 인과 모델에선 어떻게 추정하는지 다룰 예정입니다.

Reference

Peters, J., Janzing, D., & Schölkopf, B. (2017). Elements of causal inference: foundations and learning algorithms (p. 288). The MIT Press.