Causal Discovery - [1] From Graph to Causality

Graphical model로부터 어떻게 인과관계를 표현하는지 소개합니다.

Graphical Models

그래프를 이용해 인과관계를 표현해봅시다.

DAG와 PDAG

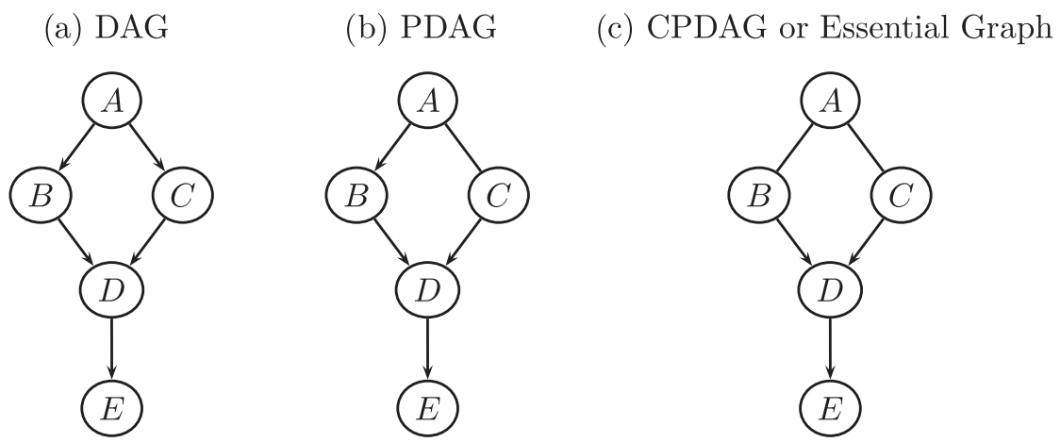
그래프 모델 중 하나는, DAG 입니다. DAG (Directed Acyclic Graph) 는 방향성이 있고 순환성이 없는 그래프 입니다. 우리가 인과관계를 표현하기 위해 DAG가 왜 필요했는지를 생각해본다면, 방향성은 어떤 것이 원인이고 어떤 것이 변수인지를 명료하게 하기 위해 필요하고, 비순환성은 인과관계가 순환되어 무엇이 원인인지 알기 어렵게 하는 것을 방지하고자 하는 것입니다. 예를 들면, 닭이 먼저인지 달걀이 먼저인지를 명확하게 하고자 함입니다.

DAG에 특정 변수 쌍에는 directed path가 없는 그래프가 존재합니다. 이를 부분적으로 DAG인 PDAG (Partially DAG) 라 합니다.

CPDAG (Completed Partially DAG) 는 PDAG 중 모든 MEC를 포함하는 그래프로 PDAG 중에서도 조건부 독립성 특성이 같이 구별할 수 없는 그래프를 말합니다. 여기서 얘기된 MEC와 조건부 독립성은 아래에서 다시 살펴봅니다.

DAG에 노드들의 랜덤성(확률)을 표현하면 BN이 됩니다. BN (Bayesian Network) 은 랜덤변수들 사이의 조건부 독립성을 DAG로 표현한 확률적 그래프 모델 입니다.

Probabilistic Graphical Models

BN에 변수 간 영향 정도를 함수적 관계로 표현하고자 한 모델이 SCM입니다. SCM (Structural Causal Model) 은 확률적 그래프 모델인 BN에 랜덤변수 간 함수적 관계를 가정한 모델을 말합니다. 이로부터 SCM은 인과관계를 이해하기 위해서, 변수들이 서로 어떻게 관련있고, 또 상호작용하는지를 설명하는 도구가 되었습니다. (다음 포스트에서 더 자세히 살펴보겠습니다.)

여기서 주목해야할 점은, Causal Discovery 방법에 따라 필요한 그래프가 다를 수 있다 는 점입니다. Causal Discovery가 여러 배경에서 연구가 되었는데, DAG(PDAG, CPDAG)만을 가정하거나, BN만을 가정하거나, SCM까지 가정한 알고리즘들이 존재합니다.

아래 그림에서 그래프로부터 인과관계를 어떻게 표현하는지 정의하고자 합니다.

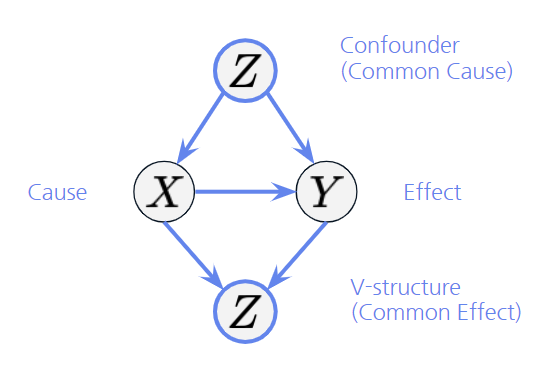
• X -> Y 만 보면 X는 Y의 Cause, Y는 X의 Effect 라 합니다.
• X <- Z -> Y를 보면 Z는 X와 Y 사이의 Confounder (Common Cause) 라 합니다.
• X -> Z <- Y를 보면 Z는 X와 Y 사이의 V-structure (Collider, Immorality, Common Effect) 라 합니다.

Conditional Independence

Causal Discovery, 즉 그래프를 식별(identify)하기 위해 조건부 독립성 특성을 이용하는 방법이 있습니다. 이 방법을 추후 설명하고, 이를 위한 조건부 독립성 특성에 대해 살펴봅니다.

세 변수 $X, Y, Z$에서 $Z$가 주어졌을 때, $X$의 조건부 분포는 $Y$의 조건부 분포에 대해서 독립적입니다:

\[p(X,Y|Z)=p(X|Z)p(Y|Z)\]

이를 조건부 독립성 (Conditional Independence) 라고 하며 다음과 같이 표기합니다: $X \perp !!! \perp Y \mid Z$

Three Graph Structures

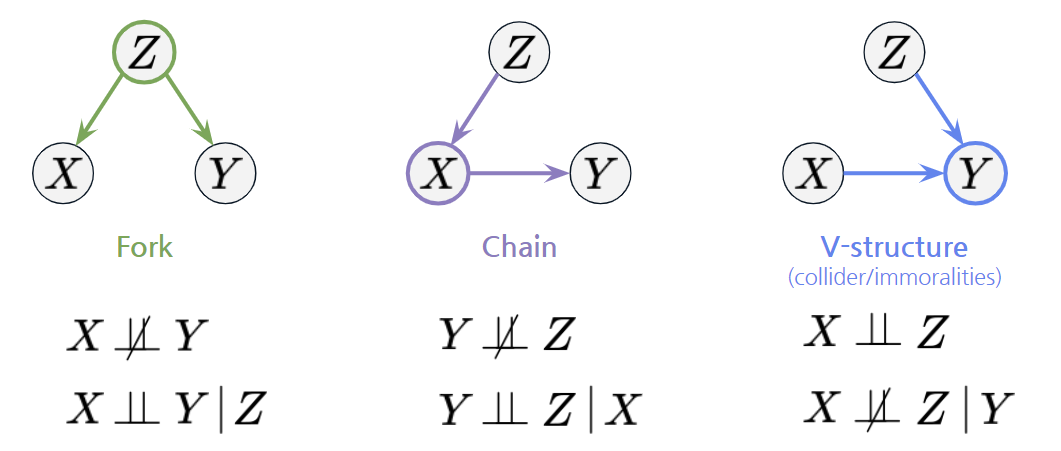
조건부 독립성 특성을 이용했을 때, conditioning에 따라 (조건부) 독립성 특성이 다른 특이한 그래프 구조가 3가지 있습니다. 그래프의 조건부 독립성 구조를 이용해 인과관계를 찾아낼 수 있습니다

먼저 Fork 구조입니다. Fork 구조에서는 X와 Y가 Z에 의해 조건부 독립입니다. X와 Y만 보면 둘은 서로 영향이 있는 것(종속)처럼 보이지만, Z를 조건부로 두게 되면, X와 Y는 서로 독립이 됩니다.

Chain 구조는 Fork 구조와 조건부 독립성 특성이 같습니다. X와 Z만 보면 둘은 Z에서 X를 거쳐 Y에 영향을 주는 것(종속)처럼 보이지만, 중간 매개재 X를 조건부로 두면 서로 독립이 됩니다.

V-structure 구조는 위와 반대입니다. X와 Z만 보았을 때는 서로 영향이 없는 것 같지만, Y를 조건부로 두게 되면, X와 Z는 서로 종속이 됩니다. 이 구조가 가장 중요한데, 바로 아래에서 그 이유를 살펴보겠습니다.

어떤 변수를 조건으로 두었는지(conditioning)에 따라 종속이었다가, 독립이기도 한 특성을 활용해 우리는 그래프의 구조를 Fork, Chain, V-structure 등으로 특정지을 수 있어, 인과관계를 찾을 때에 유용하게 활용할 수 있습니다.

Markov Equivalence Class (MEC)

조건부 독립성 특성을 이용하여 인과 그래프를 살펴볼텐데, 이 특성을 이용해도 그래프를 특정짓지 못하여 Causal Discovery를 못하는 경우가 발생합니다.

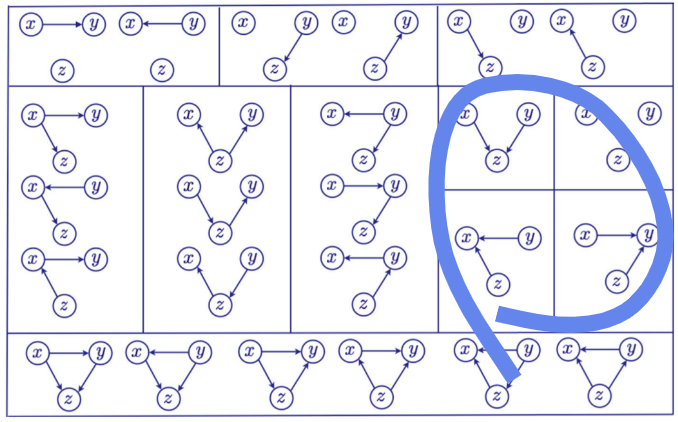
MEC (Markov Equivalence Class)는 조건부 독립성 특성이 같은 그래프 집합을 말하며, 독립성 특성이 같으므로 그래프를 unique하게 특정짓지 못하게 됩니다. 아래 그림에서 하나의 네모 박스 안에 있는 모든 그래프는 같은 조건부 독립성 특성을 가지는 것을 의미합니다. 예를 들어, 맨 왼쪽 가운데 박스에는 하나의 박스에 3개의 그래프가 있으며, 이 세 그래프는 모두 같은 조건부 독립성 특성을 가집니다. 다만, 맨 오른쪽 가운데 4개의 박스는 모두 하나의 박스 안에 하나씩의 그래프만 가집니다. 모든 노드가 독립인 박스를 제외하면 모두 V-structure를 가집니다. 즉, V-structure를 가진 그래프는 모두 MEC인 그래프가 오직 하나만 존재하기 때문에, 그래프를 Unique하게 특정지을 수 있습니다.

Reference

Pearl, J., Glymour, M., & Jewell, N. P. (2016). Causal inference in statistics: A primer. John Wiley & Sons.

Bishop, C. M., & Nasrabadi, N. M. (2006). Pattern recognition and machine learning (Vol. 4, No. 4, p. 738). New York: springer.

Eberhardt, F. (2017). Introduction to the foundations of causal discovery. International Journal of Data Science and Analytics, 3, 81-91.

Alonso-Barba, J. I., Gámez, J. A., & Puerta, J. M. (2013). Scaling up the greedy equivalence search algorithm by constraining the search space of equivalence classes. International journal of approximate reasoning, 54(4), 429-451.