On Causal and Anticausal Learning
Summary: Prediction 방향에 따라 Causal learning과 Anticausal learning이 있다. Semi-supervised Learning의 경우 causal이 아닌 anticausal learning에서만 작동한다.
통계적 상관성은 우리가 알지 못하는 Causal structure 때문에 발생합니다. Causal model이 statistical model보다 더 많은 정보를 가지기 때문이죠. 이는 어떤 경우에서는 결합분포의 비대칭성을 통해 알 수 있습니다. 이 논문에서는 이에 대해 초점을 맞추고 그 의미에 대해 알아보고자 합니다. 즉, Causal model 중 functional view가 가능한 SCM을 통해 우리는 예측의 방향이 중요함을 보일 것입니다.
1. Background
Notation
\(C,E\)는 각각 Cause, Effect이며, \(\mathcal{C},\mathcal{E}\)는 각각 \(C,E\)의 domain입니다.
\(X\)는 input, \(Y\)는 output이고 각각 cause 혹은 effect에 해당되며,
joint distribution을 \(P_{C,E}(c,e)\), marginal distribution \(P_C(c),P_E(e)\)이라 합니다.
Assumptions
Causal sufficiency
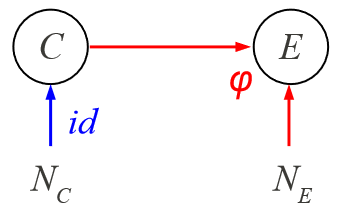
두 독립적인 노이즈 변수 \(N_C,N_E\)는 분포 \(P(N_C),P(N_E)\)를 가집니다. 함수 \(\varphi\)와 \(N_E\)는 서로 독립적으로 \(P(E|C)\) 를 결정합니다. 즉, \(E=\varphi(C,N_E)\)가 됩니다. 이때, \(P(E|C)\) 를 cause \(C\)에서 effect \(E\)로 변환하는 매커니즘이라 합니다.
Independence of mechanism and input
메커니즘이 cause의 분포와 독립이라고 가정합니다. 즉, \(P(E|C)\) 와 \(P(C)\)는 서로에 대한 정보를 가지고 있지 않습니다. 이를 통해 causal model을 안다면 input의 변화에 더 robust할 수 있다고 생각할 수 있습니다. (예로, 유전자 서열의 접합 패턴을 예측할 때 기본적인 접합 메커니즘은 일정할 것이고 종(species)에 독립입니다.)
독립 가정은 cause와 effect의 비대칭성을 유도할 수 있습니다. 즉, \(P(C)\)와 \(P(E|C)\) 는 독립이나, \(P(E)\)와 \(P(C|E)\) 는 독립이 아닙니다.
Richness of functional causal models
이변량 functional causal model은 충분히 (function class가) rich해서 causal direction이 추론될 수 없습니다. conditional independence만으로 causal discovery가 보통 안되지만 PC algorithm 등 추가가정을 덧붙이면 어떤 경우에서는 될 수 있습니다. 따라서 이러한 가정은 중요한데 이러한 것들이 메커니즘의 노이즈에 대한 민감도를 컨트롤 함으로써 복잡성까지 조절할 수 있습니다.
Additive noise models (ANMs)
\(\phi\)는 linear model, \(N_E\)는 Gaussian distribution 이라 가정하면, ANM 모델은 다음과 같습니다.
\(\begin{align*}E=\varphi(C,N_E)=\phi(C)+N_E\end{align*}\) ANM은 residual noise 변수가 cause와 독립이도록 하면서 cause에 effect를 regressiong함으로써 fitting 시킵니다.
이 논문에서 ANM은 중요합니다: 1) causal discovery를 하고, 2) ANM을 일반화해서 \(\phi\)를 share하는 형태의 모델을 구축하여, causal direction의 영향성을 볼 것입니다.
이전 work에서 C,E의 common effect에 따른 sample selection으로 데이터를 얻었을 때, P(C)와 \(P(E|C)\) 가 모두 변하는 시나리오, 혹은 데이터가 C,E의 common cause에 따라 달린 경우를 살펴보았음. 또 다른 이전 work에서는 다른 도메인/데이터셋을 의미하는 $S$를 도입하여 $S$가 causal/statistical statements를 도메인간 transfer하는게 연관있는지를 나타냅니다. 이 transportability는 조건부 독립성이 메커니즘의 불변성을 의미할 수 있습니다.
2. C → E or E → C ?
이번 챕터에서는 cause로부터 effect를 예측하는지 effect로부터 cause를 예측하는 상황인지에 따라 달라지는 예측 효과를 보여주고자 합니다. 즉, \(X\)로부터 \(Y\)를 예측할 때 causal/anticausal direction에 따라 어떻게 \(P(Y|X)\) 를 추정할 수 있는지를 소개합니다. 이를 요약하면 다음과 같습니다.
1. Causal direction에서,
Covariate shift (\(P(X)\)가 바뀌는 경우): 메커니즘 \(P(Y|X)\) 가 독립성 가정에 의해 영향을 받지 않습니다.
Semi-supervised learning: \(P(X)\)가 \(P(Y|X)\) 에 대한 정보를 포함하지 않기 때문에 불가능합니다.
Transfer learning (\(\phi\)는 바뀌지 않고 노이즈는 바뀌는 경우): \(N_X\perp\!\!\!\perp N_Y|\text{condition}\) 인 ANM에서는 가능합니다.
2. Anticausal direction에서,
Covariate shift (\(P(X)\)가 바뀌는 경우): \(P(X)\)의 변화가 메커니즘인 \(P(X|Y)\) 때문인지, cause 분포인 \(P(Y)\) 때문인지를 결정해야 합니다.
Semi-supervised learning: \(P(X)\)가 \(P(Y|X)\) 에 대한 정보를 가지고 있으므로 가능합니다.
Transfer learning: 위와 같습니다.
2-1. C → E : Predicting Effect from
\(X\)로부터 \(Y\)를 예측할 때, \(X\)가 cause이고 \(Y\)가 effect인 경우(causal direction을 가질 때)를 causal prediction 이라고 합니다. 이 경우 모델의 노이즈의 변화에 대해 추정이 얼마나 robust한지에 관심이 있습니다. 다음과 같은 상황들을 살펴볼 것입니다.
2-1.1. Additional information about the input
Robustness w.r.t input changes
\(P(X,Y)\)과 \(P'(X)\ne P(X)\)로부터 추가로 샘플링된 데이터로부터 학습할 때, \(P'(Y|X)\) 을 추정하자.
이 경우, causal direction, 즉 \(X\xrightarrow{} Y\)인 상황입니다. 이때 메커니즘과 input의 독립성때문에, \(P(X)\)의 변화로 \(P(Y|X)\) 를 변경시킬 수 없습니다. 따라서, \(P'(Y|X)=P(Y|X)\) 라고 결론지을 수 있습니다. 이런 경우를 covariate shift 라고 합니다. 그러나 이것이 X로부터 Y를 예측하는 rule로부터 새 input 분포 \(P(X)\)에 적용될 필요가 없다는 것을 의미하지는 않습니다. 왜냐하면, \(P(X)\)가 높은 확률을 가진 곳에서 데이터가 잘 피팅하지만 \(P'(X)\)가 높은 곳에선 그렇지 않을 수 있기 때문입니다.
Semi-Supervised Learning
\(P(X,Y)\)과 \(P(X)\)로부터 추가로 샘플링된 데이터로부터 학습할 때, \(P(Y|X)\) 를 추정하자.
1에서 얘기했듯이, 메커니즘과 input의 독립성에 의해 \(P(X)\)가 \(P(Y|X)\) 의 정보를 포함하지 않습니다. 따라서 다른 input을 추가해도 영향이 없을 것입니다. 즉, 새로운 (unlabeled) input을 추가하여 학습하고자 하는 Semi-Supervised Learning에서는 Causal Prediction은 의미가 없습니다.
2-1.2. Additional information about the output
Robustness w.r.t. output changes
\(P(X,Y)\)와 \(P'(Y)\)로부터 추가로 샘플링된 데이터로부터 학습할 때, ** \(P'(Y|X)\) **를 추정하자.
여기서 가정은 not clear!
\(P(X)\)나 \(P(Y|X)\) 가 바뀌는지 아닌지를 결정해야 합니다 (4번의
Localizing distribution change). \(P(X)\)가 바뀌면 2.1.1대로 covariate shift 상황입니다. 다만, \(P(Y|X)\) 가 바뀌면 \(P'(Y|X)\) 를 4번의Estimating causal conditionals로 추정해야 합니다. 여기서 additive noise는 충분 조건입니다.Additional outputs
\(P(X,Y)\)과 \(P(Y)\)로부터 추가로 샘플링된 데이터로부터 학습할 때, ** \(P(Y|X)\) **를 추정하자.
가정: \(P(X,Y)\)는 \(X\xrightarrow{}Y\)인 additive noise model을 가지고, \(P(Y)\)는 \(Q*R\)로 유일하게 분해된다. (예를 들어, noise가 Gaussian이고 \(P(\phi(C))\)가 분해될 수 없다면 만족한다)
추가된 output은 분해했을 때 \(P(N_Y)=Q\) 또는 \(P(N_Y)=R\)이므로 도움이 되는 정보입니다. additive noise model은 그 대안이 맞는건지 아닌지를 말해줍니다. \(P(Y)\)를 알면, \(P(Y|X)\) 를 학습하는 것은 \(x,y\) pair로부터 \(\phi\)를 학습하게 되는데, 이는 더 약하고 일반적인 문제입니다.
2-1.3. Additional information about the input and the output
\(P(X,Y)\)과 \(P'(X,Y)\)로부터 추가로 샘플링된 데이터로부터 학습할 때, ** \(P'(Y|X)\) **를 추정하자.
Transfer Learning (only noise changes)
가정: additive noise, \(\phi\)는 불변이나, noise는 변한다.
이 경우, 하나의 함수를 출력하는
Conditional ANM을 수행합니다. 이는 두 데이터셋을 분리해서 잔차의 독립성을 강제합니다. causal direction은 한 데이터로부터 다른 데이터로 지식을 transfer하는 데에 중요합니다.Concept drift (only function changes)
가정: ANM. \(N_X,N_Y\)는 불변이나, \(\phi\)가 변한다.
\(\phi\)를 얻기 위해 \(P'(X,Y)\)로부터 샘플된 데이터에 ANM을 수행하고 \(P'(Y|X)=P_{N_Y}(Y-\phi(X))\) 를 구합니다.
2-2. E → C : Predicting Cause from Effect
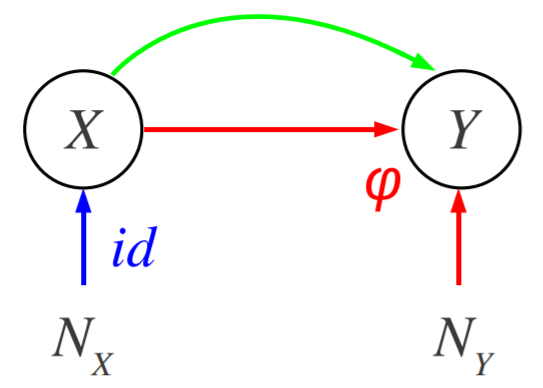
\(X\)로부터 \(Y\)를 예측할 때, \(X\)가 effect이고 \(Y\)가 cause인 경우(anticausal direction을 가질 때)를 anticausal prediction 이라고 합니다. 이 경우 \(P(X|Y)\) 가 causal 메커니즘이겠죠. 이는 독립성 가정에 의해 \(P(Y)\)와 독립입니다. 반면에, \(P(Y|X)\) 는 \(P(Y)\)의 변화에 민감할텐데, 이를 추정하는 것은 \(P(X|Y)\) 를 모델링하고나서 베이즈룰을 이용해 \(P(Y|X)\) 를 만드는게 나을 것입니다.
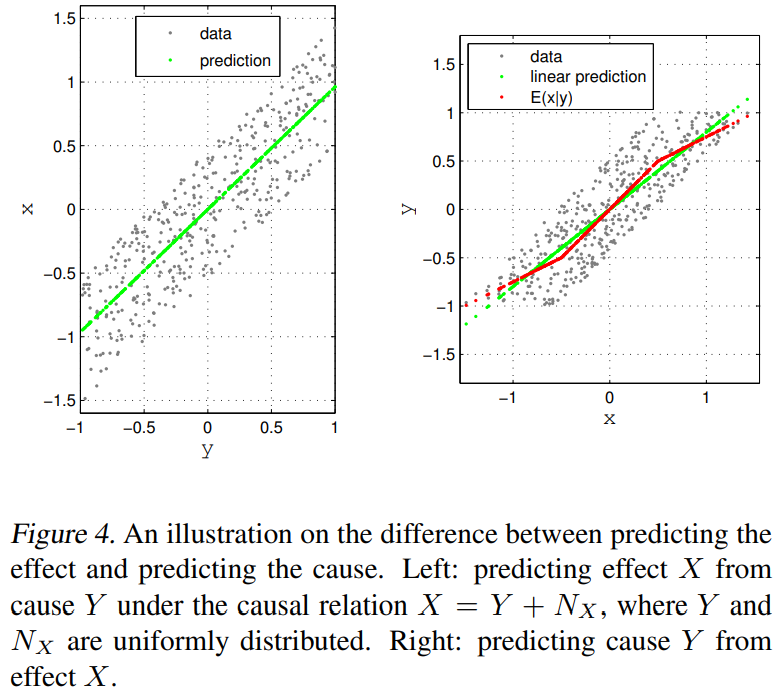
예로, \(X=Y+N_X\)가 있고 \(Y\perp\!\!\!\perp N_X\)라고 합시다. 아래 그림을 보면 되는데, \(\mathbb{E}(X|Y)\) 는 $Y$에 대한 linear이면 \(P(X|Y)\) 를 잘 설명할 수 있을 것입니다. 그러나 그게 아니라 복잡하다면, 그 모양이 \(P(Y)\)에 따라 달라질 것입니다.
2-2.1. Additional information about the input
Robustness w.r.t input changes
\(P(X,Y)\)과 \(P'(X)\)로부터 추가로 샘플링된 데이터로부터 학습할 때, ** \(P'(Y|X)\) **를 추정하자.
가정: addifive Gaussian noise, 역함수가 존재하는 \(\phi\), 분해 불가능한 \(P(\phi(Y))\)는 sufficient하다. 그리고 \(P(X|Y)\) 는 invertible하다.
이 경우, \(P(Y)\)나 \(P(X|Y)\) 중 무엇이 바뀌는지 결정하고,
Localizing distribution change를 적용합니다. \(P'(Y)\)는 \(P(X|Y)\) 가 injective conditional이라고 가정하고Inverting conditionals로 추정합니다. \(P'(X,Y)\)를 얻어서 \(P'(Y|X)=P'(X,Y)/\int P'(X,Y)dY\) 를 계산합니다. 반면에 \(P(X|Y)\) 가 바뀐다면 \(P'(X|Y)\) 를Estimating causal conditionals로 추정합니다.
결과적으로, Causal direction에서는 Semi-supervised learning이 불가능하지만, Anticausal direction에서는 가능합니다.
References
Schölkopf, B., Janzing, D., Peters, J., Sgouritsa, E., Zhang, K., & Mooij, J. (2012). On causal and anticausal learning. arXiv preprint arXiv:1206.6471.