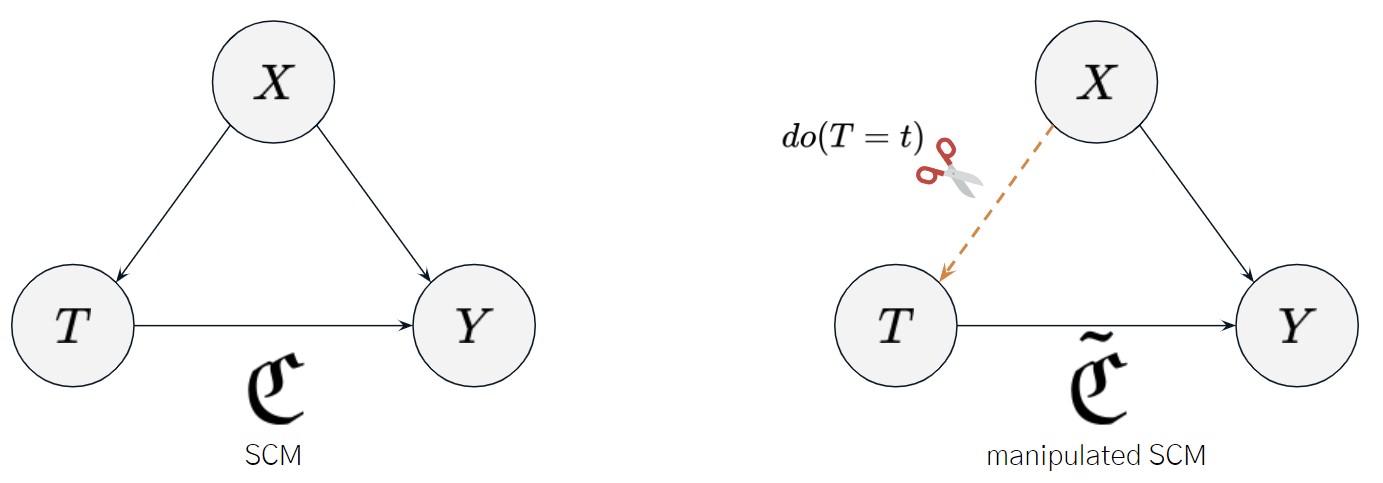Causal Discovery - [2] Structural Causal Model

Summary Causal Discovery를 위한 표현인 Structural Causal Model, 즉 SCM에 대해 소개합니다. Causal Discovery 관련 내용은 이전 글을 참조해주세요.

Pearl’s Causal Hierarchy

Pearl 교수님은 3가지의 사다리와 각각의 level을 정의하였습니다.

Level	Name	Activity	Symbol	Questions
L1	Association	관측(Seeing)	$P(y\mid x)$	“What if I see …?”
L2	Intervention	실험(Doing)	$P(y\mid do(x))$	“What if I do …?”
L3	Counterfactual	회고(Imaging)	$P(y_x\mid x’,y’)$	“What if I had done …?”, “Why?”

Observation

L1은 Association, 즉 관측(observation)된 데이터만으로 물음에 답하고자 하는 것입니다. 예를 들어 “아스피린을 복용했을 때 내 두통을 줄이는 효과가 있었는가?”와 같은 질문입니다. 조건부 분포($P(y\mid x)$)로 표현합니다.

Intervention

L2는 Intervention, 즉 실험(intervention)을 통해 물음에 답하고자 하는 것입니다. 예를 들어 “아스피린을 먹는다면, 내 두통이 치료될까?”와 같은 질문입니다.

Intervention은 do-operator를 이용하여 $P(Y\mid do(X:=x))$ 혹은 $P(Y\mid do(X))$로 표현됩니다. 변수 $X$에 임의적인 변경을 가하여 값 $x$로 고정시키고, $Y$에 미치는 영향을 측정합니다. 위 예시에서 살펴보면, 아스피린 복용과 같습니다. 여기서 intervention 후 그래프는 변경(manipulated)되며, $X$에 영향을 미치는 방향성(incoming edges)은 제거됩니다.

Counterfactual

L3는 Counterfactual, 즉 회고(retrospection)를 통해 물음에 답하고자 하는 것입니다. 실제 일어나지 않았던 일을, 일어났다고 가정해보고 추정하려고 하는 것입니다. 예를 들어 “만약 저번에 아스피린을 먹지 않았었는데, 아스피린을 먹었더라면, 내 두통은 치료되었을까?”와 같은 질문입니다.

Counterfactual은 $P(Y\mid x’,y’)$로 표현하며, 실제로 $X=x’, Y=y’$라고 관측했을 때, $X=x, Y=y$로 나타났을 확률을 의미합니다.

참고로, Counterfactual에서 말하고자 하는 바는 Potential Outcomes에서의 것과 동일합니다.

그리고 Pearl 교수님은 더 낮은 레벨의 지식으로는 더 높은 레벨의 지식을 논할 수 없다 고 정의하였습니다.

With knowledge from lower layers, we cannot say anything about the higher layers.

Structural Causal Model (SCM)

SCM(Structural Causal Model)은 인과관계를 이해하기 위해서, 세상을 구성하는 변수들이 서로 어떻게 관련있고, 또 상호작용하는지를 설명하는 도구입니다.

어떻게 원인과 결과를 표현할까요? (두 변수의 경우)

가장 쉬운 경우 먼저 살펴봅시다.

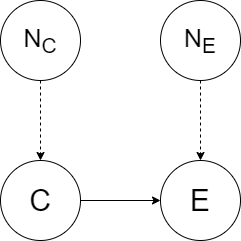
두 변수 C, E가 존재할 때, $C \rightarrow E$인 그래프를 가지는 SCM은 다음과 같은 할당(assignment)를 가집니다.

\[\begin{align} C &:= N_C \\ E &:= f_E(C,N_E) \end{align}\]

여기서 랜덤변수 C, E 중 C는 원인, E는 결과를 의미하며, $N_C, N_E$는 각각 C와 E에 대한 노이즈 변수이며, f는 함수로, 변수간 함수적 관계성으로부터 값을 결정합니다. C는 E의 direct cause, $C \rightarrow E$는 causal graph입니다.

그렇다면, 어떻게 내생/외생 변수를 모두 표현할까요? (여러 변수의 경우)

보다 일반적인 표현의 SCM을 살펴봅시다.

SCM $\mathfrak{C}:=(S,P_N)$은 다음과 같은 할당 set을 가집니다:

\[\begin{align} X_j:=f_j(PA_j,N_j), \qquad j=1,\dots,d \end{align}\]

여기서 $PA_j$는 $X_j$ 변수의 parent 를 나타내며, 관측가능한 내생 변수 를 의미합니다. $P_N$은 노이즈 변수 $N_j,j=1,\dots,d$의 결합확률분포를 나타내며, jointly independent하다고 가정합니다. 여기서 노이즈 변수는 관측 불가능한 잠재(latent) 변수인 외생 변수입니다.

SCM은 뭐가 다를까요? SCM은 단순히 그래프로 인과관계를 그려낸 것이 아니라, intervention과 counterfactual을 모두 표현할 수 있는 unified한 프레임워크라는 것일 겁니다.

SCM을 이용해 intervention을 표현할 수 있습니다.

기존 SCM $\mathfrak{C}$ 이 다음과 같을 때:

\[\begin{align} T:=f_T(X,U_T) \\ Y:=f_Y(X,T,U_Y), \end{align}\]

처치 변수 $T$에 intervention을 가하면 SCM이 manipulated 되어 $\tilde{\mathfrak{C}}$ 다음과 같게 됩니다:

\[\begin{align} T:=t \\ Y:=f_Y(X,T,U_Y). \end{align}\]

counterfactual은 potential outcomes와 같은데, SCM을 이용해 표현할 수 있습니다.

\[\begin{align} X_u(T=t) \quad = \quad X \textrm{ in the SCM } \mathfrak{C} \mid N=n_u; do(T:=t) \end{align}\]

Reference

Pearl, J., Glymour, M., & Jewell, N. P. (2016). Causal inference in statistics: A primer. John Wiley & Sons.

Glymour, C., Zhang, K., & Spirtes, P. (2019). Review of causal discovery methods based on graphical models. Frontiers in genetics, 10, 524.

Peters, J., Janzing, D., & Schölkopf, B. (2017). Elements of causal inference: foundations and learning algorithms (p. 288). The MIT Press.

Causal Discovery from Observations& Interventions, Causal Inference Course

[Session 18-3] 데이터 기반의 인과관계 발견 (Causal Discovery), Korea Summer Session on Causal Inference 2021

Causal Inference under the rubric of Structural Causal Model, Korea Summer Session on Causal Inference 2021