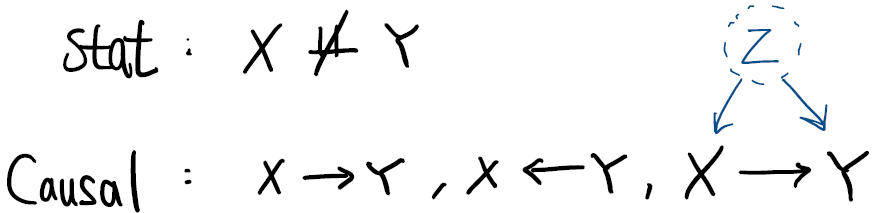Towards Causal Representation Learning

이 논문은 나온지 한 달 정도 된 최신의 논문으로, Causal Learning을 위한 방향들, 그리고 중요한 가정과 이를 이용해 할 수 있는 태스크들을 소개하였습니다. 전체적으로 기존의 ML과 달리 Causal Learning이 할 수 있는 것들을 비교하며 무엇이 가능하게 했는지 기술하고 설명하였습니다. 이 글에서는 이 논문에 대해 소개하고자 합니다.

1. Intro

Machine Learning에서 가장 중요한 것은 Generalization이었습니다. 데이터에서 다른 데이터로, 한 문제에서 다른 문제로 일반화가 잘 되는 것이 목표였지만 기존의 ML에서는 이러한 것들을 다루기엔 어려웠으므로 필요없는 것으로 여기고 i.i.d. 가정을 도입해 그 효과를 제거하였습니다. 이러한 것들로 인해 머신러닝의 몇 가지 해결해야 할 이슈들이 존재하였습니다.

첫째, Robustness입니다. 실제 데이터가 오는 분포에 대한 컨트롤이 가능한 상황은 거의 적습니다. 비전을 예로 들면, 테스트 분포가 학습 분포에서와 달라졌다거나, 카메라에 블러나 노이즈가 생겼거나, 이미지나 영상의 압축 품질이 변했거나, 물체의 이동, 회전, 뷰포인트가 변하였다는 등의 경우가 있습니다. Causal Learning에서는 intervention을 통해 이를 해결하고 일반화를 잘 하고자 하는데, 구체적으로 공간을 바꾸고, 블러나 밝기, 대조 등을 변경하고, 배경, 여러 환경의 이미지 등을 바꾸는 등을 수행할 수 있습니다. 이러한 intervention을 통해 기존의 ML/DL 모델이 가진 inductive bias에 대한 인사이트를 얻을 수 있다고 하는데, 아마 어느 변수에 어떤 intervention을 가함으로써 무엇이 변하는지 등을 알 수 있기 때문인 것 같습니다.

둘째, Learning Reusable Mechanisms는 모델이 새로운 태스크나 시나리오에서 학습한 지식과 사용한 방법을 재사용한다면, 다른 상황에서도 기존의 지식을 적용하고 이와 통합할 수 있습니다. 이는 인간의 매커니즘과 비슷하게 작동하므로일반화를 잘 할 수 있게 됩니다. 이 또한 intervention으로 새로운 분포의 상황에서도 robust하게 예측이 가능합니다.

셋째, Causality Perspective는 기존의 ML이 알 수 없는 인과관계에 대한 것으로, 이를 통해 우리는 관측했던 상황보다 다른 상황에 있어도 상상하고 추론할 수 있도록 하며, 더 robust한 지식을 얻을 수 있고, 궁극적으로 reasoning이 가능하도록 할 수 있습니다.

위에서 얘기한 이슈들은 모두 causal approach로 가능할 수 있습니다.

특히, intervention을 통해 변화를 허용하는 데이터 생성 프로세스에 대한 지식을 표현하게 됨으로써 해결할 수 있습니다. 따라서 궁극적으로 Konrad Lorenz의 imagined space의 형태와 가까워지고자 합니다. 이 논문에서는 causal learning에 대한 전체적인 기술을 causal modeling, 필요한 가정과 어려운 점들, 그 중 핵심 가정인 ICM principle과 이를 확장한 SMS hypothesis, causal discovery와 inference 방법, 그리고 현대 ML에의 적용 순서대로 설명하고 있습니다.

2. Towards Causal Representation Learning

2-1. Levels of Causal Modeling

예시로, coupled differential equations modeling physical mechanisms for evolution에 대한 설명이 있었습니다만, 잘 모르겠습니다.. ㅠㅠ

이 챕터에서는 Causal Modeling을 위해 어떤 수준들을 고려해야 하는지 설명하고 있습니다.

먼저, i.i.d. 세팅에서 예측하고자 할 때, 기존 ML에서는 상관관계로 대표되는 통계적인 유의성에 의해 예측을 합니다만, 이는 동일한 실험 조건을 가져야 한다는 가정이 기저에 깔려있습니다. 그러나 Causal 에서는 정확도가 높은게 다가 아니라 인과관계를 모델링하려 하므로 인과관계는 없지만 유의한 변수 등의 문제를 해결할 수 있습니다. 이는 intervention을 수행하면 데이터의 분포가 바뀌므로 이를 다룰 수 있게 됩니다. 예를 들어, ‘황새 개체군이 증가하면 출생률이 증가한다’는 높은 상관관계를 가지지만 인과관계를 가지지 않습니다. 이는 intervention인, 황새 개체군을 변화시켰을 때, 출생률에 영향을 미치는지 확인함으로써 가능하게 됩니다. 또한, 추천 시스템 등에서 노트북을 보유한 사람이 노트북 가방을 사고자 하였으나, 노트북을 새롭게 추천하는 causal 관계를 반대로 예측하는 경우를 예시로 들 수 있습니다.

둘째, 분포 변화(distribution shifts)를 예측할 수 있습니다. 기존 ML과 달리 Causal Leanring은 intervention이 가능한데, 이는 변수들의 값, 관계에 영향을 주고 이로 인해 변수들의 결합 분포를 바꿀 수 있습니다. 이를 통해 실험 조건이나 데이터의 분포가 바뀌어도 robust하게 예측할 수 있습니다. 예를 들어, ‘출생률을 조정할 수 있는 나라에서 황새 개체수가 증가하는가?’, ’담배가 안 좋다는 인식이 있다면 사람들이 담배를 덜 피나?’, 와 같은 질문에 intervention을 가함으로써(출생률을 조정하거나(!), 담배에 대한 인식을 바꿈) 예측할 수 있습니다.

셋째, counterfactual question들을 다룰 수 있습니다. counterfactual은 일이 일어난 이유에 대한 회고적 추론과 이후 다른 행동의 결과를 상상하고 원하는 결과를 얻을 수 있는 것으로 우리는 이러한 것들을 통해 이유를 유추하고 다음 행동을 결정할 수 있습니다. 이는 agent가 자신의 의사결정을 반영하고 검증할 가설을 공식화할 수 있으므로 RL에서 중요합니다. 예로, 기존의 interventional question은 ‘환자가 정기적으로 운동한다면 심부전 확률이 낮아질까?’ 라면, counterfactual question은 ‘환자가 일년만 일찍 운동을 시작했다면 심부전을 앓았을까?’ 로 생각할 수 있습니다.

넷째, Data들의 종류를 나누고 Causal Learning이 가능한 데이터를 정의합니다.

첫번째 분류로 observational data와 interventional data입니다. obs. data는 우리가 기존에 알고 있는 i.i.d. 를 가정한 데이터이고, interventional data는 알려진 intervention을 가지며, intervention의 결과인 여러 분포에서 샘플링된 데이터셋을 관찰하여 domain shifts나 알려지지 않은 intervention이 있을 수 있습니다.

두번째 분류로, hand-engineered data와 raw (unstructured) perceptual input data가 있습니다. raw data는 unstructured(graph 구조가 없음)으로, causality에 대한 direct information이 없는 우리가 기존에 알고 있는 보통의 데이터이고, hand-engineered data는 structured되며 high-level에서 의미적으로 causal 관계가 있는 변수들을 가진 데이터를 의미합니다.

마지막으로 데이터 수집 측면에서, 우리는 causal learning이 가능하면서 더 많지만, 여러 환경이나 intervention을 수행할 수 있는 데이터를 모아야 합니다. 이 또한 meta-learning 등의 방법을 통해 대체되는 방법들을 최근 연구에서는 찾고 있는 것 같습니다.

2-2. Causal Models and Inference

이번 파트에서는 causal inference를 가능하게 하기 위한 causal model의 기본 세팅 및 가정을 설명합니다.

기존의 ML은 i.i.d. 데이터로부터 risk를 최소화할 수 있도록 보장이 되었지만, i.i.d. 가정이 깨진 데이터에서는 성능이 많이 떨어질 수 있습니다.

또한, 관측되지 않은 잠재(latent) 변수가 존재할 수 있습니다. 여기서 이는 confounder일 수 있고 confounder는 다른 두 변수를 유의하게 보이도록 하지만 실제로는 causally 관계있지는 않습니다.

intervention은 여기서 \(U_i\)를 바꾸거나, \(f_i\)를 상수로 지정하거나, 아예 functional form을 바꾸는 것을 의미합니다. 이에는 여러 종류가 존재하는데, 특히 hard/perfect intervention은 함수를 상수로 고정하는 것을, soft/imperfect intervention은 함수나 노이즈 항을 다른 새로운 것으로 바꾸는 것을 의미하며, uncertain intervention은 어떤 메커니즘이나 변수에 intervention을 가해야 하는지 혹은 영향을 받을지 모르는 것을 의미합니다.

그리고, Causal inference를 위해 intervention을 가하는데, 이를 위해 중요한 원칙인 The Reichenbach Principle (Common Cause Principle) 을 설명합니다. 이는, Causal Learning을 통해 confounder의 존재 등을 알 수 있게 되어, 더 많은 설명이 가능하게 됩니다.

Common Cause Principle:

If two observables X and Y are statistically dependent, then there exists a variable Z that causally influences both and explains all the dependence in the sense of making them independent when conditioned on Z.

Structural Causal Models (SCMs)

causal model의 가능한 후보군들에는 DAG(Directed Acyclic Graph), CGM(Causal Graphical Models), SCM이 있습니다.

관측 변수, deterministic한 함수, 설명이 안되는 랜덤 변수를 각각 \(X_i, f_i, U_i\) 로 정의합니다. 여기서 \(U_i\)는 위의 Principle에 의해 jointly independent이어야 합니다.

\[X:=f_i(PA_i,U_i), \qquad i=1,\cdots,n\]

DAG는 joint distribution을 계산하기 위해 \(X_j|PA_j \perp \!\!\! \perp ND_j\)

라는 Causal Markov condition이 필요합니다.

Causal Graphical Model은 다음과 같이 causal factorization이 가능합니다.

\[P(X_1,\cdots,X_n)=\prod_{i=1}^nP(X_i|PA_i)\]

두 그래프가 같은 조건부 독립성을 가지므로 같은 Markov equivalence class 내에 있습니다. 하지만 causal direction은 다를 수 있으므로 이 Markov 조건은 causal discovery에 충분하지 않습니다.

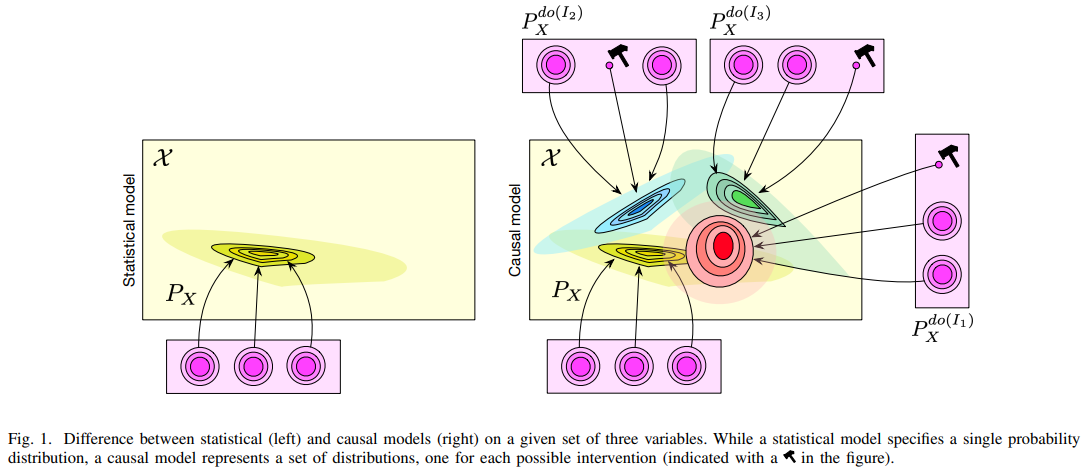
SCM은 causal variable과 structural equations 형태로 구성됩니다. DAG의 구조적 할당을 따르지만 SEM의 functional form을 통해 intervention 셋을 implictly 지정할 수 있습니다. 궁극적으로 SCM은 더 많은 상황에서의 분포를 고려할 수 있으므로 더 풍부한 function class를 가질 수 있습니다.

아래 그림처럼, 더 많은 분포를 고려할 수 있게 됩니다.

2-3. Independent Causal Mechanisms

(컴퓨터) 비전에서 빛에 포함된 정보가 뇌에 도달하는 물체의 메커니즘은 서로 독립입니다. 물체를 움직여도 전체 생성 프로세스의 다른 변수에는 영향을 주지 않습니다. 예를 들어, 고도(altitude)가 바뀌어도 고도가 온도(average of Temparature)에 미치는 메커니즘은 변하지 않습니다. 이러한 것들을 정리한 원칙이 아래의 ICM Principle 입니다.

ICM Principle

Independent Causal Mechanisms (ICM) Principle:
The causal generative process of a system’s variables is composed of autonomous modules that do not inform or influence each other. In the probabilistic case, this means that the conditional distribution of each variable given its causes (i.e., its mechanism) does not inform or influence the other mechanisms.

이는 우리가 intervention을 할 수 있는지, intervention을 통해 무엇을 알 수 있는지에 중요한 원칙입니다. 그리고 Causal 변수에 각각 intervention을 할 수 있는지는 modularity, subsystem의 autonomous 등의 개념에 중요합니다.

Causal factorization에 적용하면 principle은 각 factor \(X_i|PA_i\) 들이 독립이라는 것을 의미하는데, 이는 각 메커니즘은 \(P(X_i|PA_i)\) 는 다른 메커니즘 \(P(X_j|PA_j)\) 을 바꾸지도, 이 메커니즘을 안다고 다른 메커니즘에 대한 정보를 알게 되는 것도 아님을 의미합니다.

이는 구조적 할당(structural assignments) 중 하나를 변경해도 다른 할당들은 변하지 않고(invariant), 다른 메커니즘이 외부 영향을 받아도 causal relation은 변하지 않음(autonomous)을 의미합니다. (제가 이해하기로는 autonomous는 그런 의미인 것 같습니다..)

위의 ICM Principle을 확장하면 SMS hypothesis를 도출할 수 있습니다.

Sparse Mechanism Shift (SMS):
Small distribution changes tend to manifest themselves in a sparse or local way in the causal/disentangled factorization, i.e., they should usually not affect all factors simultaneously.

ICM Principle에서 두 메커니즘의 독립성은 두 조건부 분포가 서로에게 영향을 주지 않음을 의미합니다. 여기서 서로 독립적인 intervention을 가할 수 있음을 알 수 있습니다. 또한, 두 메커니즘의 독립성은 변수 간의 종속성을 의미하는 것은 아닙니다. ICM Principle은 랜덤 변수의 독립성을 함께 가정합니다.

2-4. Causal Discovery and Machine Learning

이번 챕터에서는 Causal Discovery를 위해 SCM을 어떻게 다루는지를 살펴볼 수 있습니다.

causal discovery는 보통 faithfulness와 같은 가정들을 도입하여 conditional independence test를 하여 수행될 수 있습니다. 그러나 이에 대한 추가 가정을 통해 function class의 complexity에 restriction을 줌으로써 minimum expected risk 로 빠르게 수렴할 수 있도록 할 수 있습니다.

그렇다면, 기존의 SCM에서는 V가 f를 선택하는 데에 유의한 역할을 하도록, 즉,

\[\begin{aligned} X&=U \\Y&= f(X,V)\end{aligned}\]

로 표현할 수 있고, 일반적인 경우인 V가 관측되지 않고 값이 랜덤으로 선택된다면 SCM을 찾기 어렵습니다. 따라서 우리는 고려할 수 있는 function class에 제약을 가함으로써 실제 causal discovery가 가능토록 만듭니다. 그의 대표적인 예로 ANM(Additive Noise Model)은 아래와 같습니다.

\[\begin{aligned} X&=U \\Y&= f(X)+V\end{aligned}\]

이는 노이즈 항을 단순히 함수 밖에서 더해줌으로써 어떤 추가 가정없이 효율적으로 function class를 줄일 수 있었습니다.

2-5. Learning Causal Variables

이번 챕터에서는 Causal learning으로 해결하려고 하는 현재 ML의 문제점과 해결 방향을 소개합니다.

Problem 1: Learning Disentangled Representations

먼저, causal learning을 통해 representation의 disentangle을 할 수 있습니다. Causal factorization은 아래와 같고 이를 통해 causal representation learning은 이를 통해 disentangle이 가능하다고 보고 있습니다.

\[P(S_1,\cdots,S_n)=\prod_{i=1}^n P(S_i|PA_i)\]

ICM Principle로 인해 노이즈와 매커니즘은 각각 독립이어야 하며 이는 다른 문제나 액션에 대해 불변이거나 독립적으로 intervention이 가능해야 함을 의미합니다. 이러한 경우 우리는 representation의 분리, 즉 disentangle이 가능토록 합니다.

SMS hypothesis는 supervision signal을 주는데, 어떤 factor가 disentangle이 가능한지는 어떤 intervention을 관측할 수 있는지에 따라 다릅니다. 다른 supervision signal은 factor의 부분집합을 알 수 있게되고, 비슷하게, 어떤 변수가 추출되고, 그들의 세분화는 어떤 distribution shifts나 intervention에 의존하게 되는지, 다른 supervision signal이 가능한지를 볼 수 있습니다.

Problem 2: Learning Transferable Mechanisms

이 논문에서는 transfer 가 가능한 메커니즘의 필요성을 기존의 ML 학습 자원의 절약을 요하면서 언급합니다. 이는 물론이고, 다른 태스크나 환경에서도 robust한 학습 모델을 만들기 위해 transfer가 가능한 메커니즘의 필요성을 말하고 있습니다.

Problem 3: Learning interventional world models and reasoning

causal representation learning은 ‘thinking as acting in an imagined space’를 지향하며, intervention과 이를 통한 reasoning 등으로 이를 실현하고자 합니다.

2-6. Implications for ML

2-6-1. Semi-Supervised Learning

이는 다음 포스팅에서 해당 논문과 함께 소개하고자 합니다!

간단히, semi-supervised learning은 causal direction이 아닌 anticausal direction(Y->X라는 cause and effect 관계가 있을 때 X->Y를 예측하는 것)에서만 작동합니다.

2-6-2. Adversarial Vulnerability

Causal Learning은 adversarial attack에서도 robust하게 학습할 수 있어야 한다. 그러나 기본적으로 adversarial example은 기존의 training distribution과 다르므로 이에 대해서도 robust하고 transferable하게 학습할 수 있는 causal mechanism을 고려할 수 있다고 한다.

2-6-3. Robustness and Strong Generalization

Robustness는 중요하다. causal learning에서는 OOD(Out-of-distribution) generalization을 위해 OOD risk를 정의하고 기존에 empirical risk 뿐만 아니라 OOD risk도 함께 줄일 수 있는 robust predictor를 학습시킬 수 있다.

2-6-4. Multi-Task Learning and Continual Learning

Multiple Task가 존재하는 상황을 가정하는 Multi-task learning과 continual learning에서 causal learning은 data-generating process을 잘 학습하기 위한 SMS hypothesis를 가정한 causal generative model을 도입한다. 여기서 각 process는 서로 다른 태스크나 환경 속에서 공유하는 어떤 representation을 통해 더 잘 학습할 수 있다는 가정을 가진다.

3. Conclusion

그동안 Causal Learning을 통해 기존의 ML이 하기 어려웠던 태스크들을 어떻게 접근함으로써 다룰 수 있게 되었는지를 소개하였다. 이제 이 다음으로 어떤 태스크 혹은 Area들이 있는지를 살펴보며 이 논문 소개를 마치고자 한다.

1. Learning Non-linear causal relations at scale

   비선형의 causal 관계를 학습하고 이를 scalable하게 키우는 것

2. Learning causal variables

   어떤 intervention이 예측에 더 robust하게 학습될 수 있는지 아는 것

3. Understanding the biases of existing deep learning approaches

   DL에서 어떤 부분이 잘 학습하게 하는지 이해하는 것

4. Learning causally correct models for the world and the agent

   RL에서 abstract state representation을 가능하도록 만드는 것

End of Documents.

Reference

1. Schölkopf, B., Locatello, F., Bauer, S., Ke, N. R., Kalchbrenner, N., Goyal, A., & Bengio, Y. (2021). Toward Causal Representation Learning. Proceedings of the IEEE.