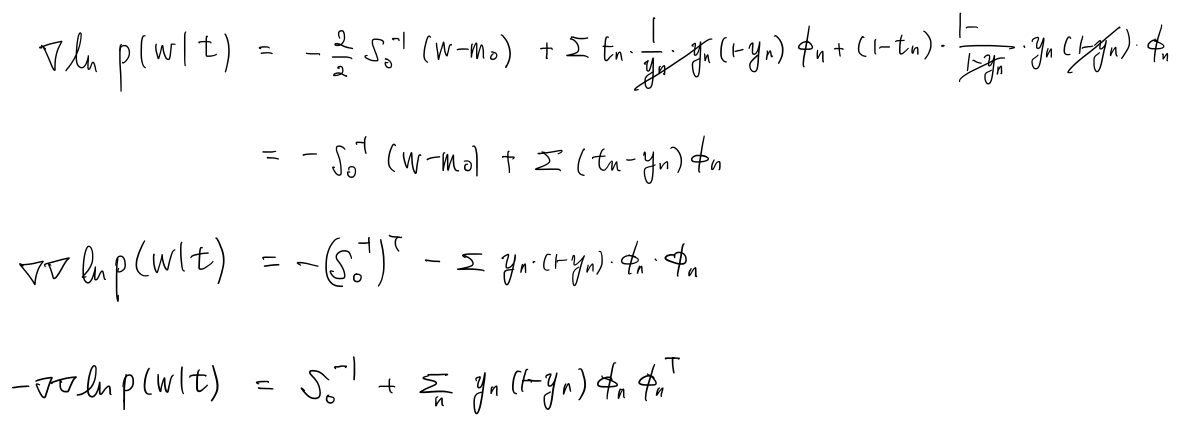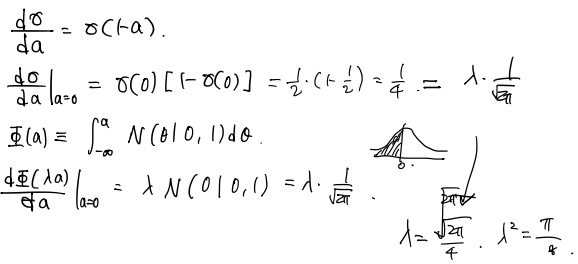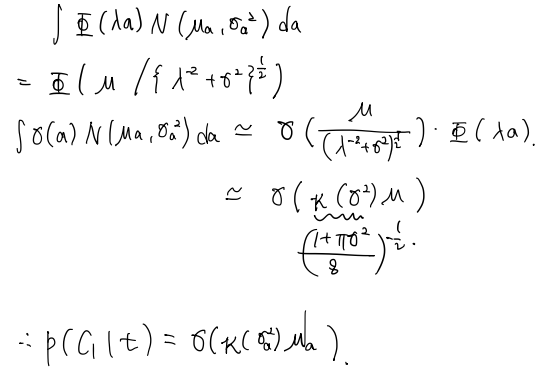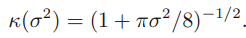Bayesian Logistic Regression
먼저, 이 글은 PRML (CH4) 공부를 바탕으로 작성된 글입니다. 따라서, 간혹 틀리다거나 더 좋은 해석이 있다면 편하게 댓글 부탁드립니다!
분류 모델인 로지스틱 회귀에 Bayesian Approach를 적용해봅시다.
Bayesian Linear Regression과 다른 점은, Gaussian Approximation을 위해 Laplace Approximation 방법을 사용한다는 것입니다.
1. Laplace Approximation
Laplace Approximation은 우리가 posterior를 구할 때 정확한 적분이 어려워 사용하는 근사 방법입니다. 구체적으로, 연속적인 변수의 집합에 대해 정의된 확률 밀도의 가우시안 근사치를 찾는 방법이며, 분포 \(p(\mathbf{z})\)의 mode를 중심으로 한 가우시안 근사 \(q(\mathbf{z})\)를 구하게 됩니다.
- 이 방법은 data 수가 많을수록 더 잘 근사합니다.
- unimodal 가우시안을 사용하며, 연속 실수 변수만 적용 가능하고, local하게 근사하여 global한 성질을 놓칠 수 있다는 점이 단점입니다.
- Laplace 근사는 다음과 같은 과정으로 수행됩니다.
- posterior의 mode 찾습니다.
- 위에서 찾은 mode를 중심(평균)으로 가지는 가우시안 분포로 근사합니다. 이때 covariance matrix는 posterior의 negative Hessian으로 구합니다.
2. Posterior Distribution
이제 posterior를 구하기 위해 Laplace Approximation을 적용해봅시다.
로지스틱 모델은 다음과 같습니다.
\[p(\mathcal{C}_1|\phi)=y(\phi)=\sigma(\mathbf{w}^\text{T}\phi)\\\sigma(a)=\frac{1}{1+\exp(-a)},\phi=\phi(\mathbf{x})\]이 경우 likelihood function은 다음과 같이 나타납니다.
\[p(\mathbf{t}|\mathbf{w})=\prod_{n=1}^N y_n^{t_n}\{1-y_n\}^{1-t_n}\\y_n=p(\mathcal{C}_1|\phi(\mathbf{x}_n))\]posterior를 구합니다.
prior는 다음과 같이 정의합니다.
\[p(\mathbf{w})=\mathcal{N}(\mathbf{m}_0,S_0)\]posterior는 Bayes’ rule을 이용해 다음과 같이 구합니다.
\[p(\mathbf{w}|\mathbf{t})\propto p(\mathbf{w})p(\mathbf{t}|\mathbf{w})\] \[\begin{aligned}\ln p(\mathbf{w}|\mathbf{t})&= \ln p(\mathbf{w})+\ln p(\mathbf{t}|\mathbf{w}) \\ &=-\frac{1}{2}(\mathbf{w}-\mathbf{m}_0)^\text{T}S_0^{-1}(\mathbf{w}-\mathbf{m}_0)+\sum \{t_n\ln y_n + (1-t_n)\ln (1-y_n)\}+constant. \end{aligned}\]posterior의 mode를 구합니다.
이제, posterior의 mode를 찾기 위해 posterior를 maximize하면, mode는 $\mathbf{w}_\text{MAP}$로 구해집니다.
이때, 해는 closed form으로 나타나지 않는데, 그 이유는 likelihood가 $\mathbf{w}$에 대해 이차 종속성을 가지므로 IRLS를 사용했던 앞 절의 내용과 유사합니다(
아마도).posterior의 negative Hessian을 구합니다.
이제, posterior의 negative Hessian을 구합니다. 여기서는 Hessian matrix만 구하면 되고 solution을 요하는 형태가 아니므로 closed form으로 나타낼 수 있습니다.
\[S_N^{-1}=-\nabla\nabla\ln p(\mathbf{w}|\mathbf{t})=S_0^{-1}+\sum y_n(1-y_n)\phi_n\phi_n^\textrm{T}\]위에서 구한 값을 이용해 Gaussian Approximation을 하면, posterior를 근사한 분포는 다음과 같이 구할 수 있습니다.
\[p(\mathbf{w}|\mathbf{t})\approx q(\mathbf{w})=\mathcal{N}(\mathbf{w}_\textrm{MAP},S_N)\]
3. Predictive Distribution
이제, 새 feature vector \(\phi(\mathbf{x}^*)\)가 주어졌을 때 분류할 클래스에 대한 예측을 시행한다고 합니다. 이를 위해 parameter에 대해 marginalize를 하여 구합니다.
\[p(\mathcal{C}_1|\phi^*,\mathbf{t}^*)=\int p(\mathcal{C}_1|\phi^*,\mathbf{w})p(\mathbf{w}|\mathbf{t})d\mathbf{w}\simeq \int\sigma(\mathbf{w}^\textrm{T}\phi^*)q(\mathbf{w})d\mathbf{w}\]그리고, 다음과 같은 과정으로 계산합니다.
\(y=\sigma(\mathbf{w}^\textrm{T}\phi^*)\)를 계산하면,
\[\begin{aligned}\sigma(\mathbf{w}^\textrm{T}\phi^*)=\int\delta(a-\mathbf{w}^\textrm{T}\phi^*)\sigma(a)da \\ \delta(\cdot): \text{dirac delta function}\end{aligned}\]따라서 posterior는,
\[\begin{aligned}p(\mathcal{C}_1|\phi^*,\mathbf{t}^*)\simeq \int\sigma(\mathbf{w}^\textrm{T}\phi^*)q(\mathbf{w})d\mathbf{w}=\int\sigma(a)p(a)da\\ p(a)=\int\delta(a-\mathbf{w}^\textrm{T}\phi^*)q(\mathbf{w})d\mathbf{w}\end{aligned}\]- 이때, $\delta$로 인해 $\mathbf{w}$에 대해 선형 제약 조건을 받으므로, $q(\mathbf{w})$를 $\phi^*$에 대해 직교하는 모든 방향으로 적분하여 marginal $p(a)$를 계산할 수 있습니다. 계산되는 분포는 모두 가우시안이므로 $p(a)$도 가우시안 형태로 될 것이며 다음과 같이 평균과 분산을 계산합니다.
Predictive Distribution 구하기
따라서, 위를 이용해 구한 예측분포는 다음과 같습니다.
\[p(\mathcal{C}_1|\phi,\mathbf{t})\simeq\int\sigma(a)p(a)da=\int\sigma(a)\mathcal{N}(a|\mu_a,\sigma_a^2)da\]probit function을 이용한 예측분포 구하기
위의 예측분포는 실제로는 analytical하게 계산하기 어렵습니다. 따라서, activation function(link function)을 inverse probit function으로 사용합니다.
\[\sigma(a)=\Phi(\lambda a)\]그 과정은 아래와 같습니다.
Reference
- Bishop, C. M. (2006). Pattern recognition and machine learning. springer.