ECI-2. Assumptions for Causal Inference

2. Assumptions for Causal Inference

Elements of Causal Inference: Foundations and Learning Algorithms 라는 책을 공부하고 (가능한 한) 제 표현으로 정리한 글입니다.

이번 챕터에서는 Causal Inference에서 중요한 원칙에 대해서 소개합니다. 사실, Causal Inference란건 굉장히 어려워서 이를 가능케 하도록 가정들을 많이 추가하게 되는데 이것들이 Real World에의 적용을 어렵게 만들 수 있어 잘 알아두는 것이 좋습니다. 학계에서는 이를 완화하려는 연구도 많이 하고 있습니다.

먼저 컴퓨터 비전 문제 예시로 독립성(Independence)에 대해서 생각해볼까요.

우리가 물체를 인식(perception)할 때, 빛이 물체로부터 반사되어 우리 눈을 통해 뇌로 전달됩니다. 그리고 우리가 물체를 보든 아니든 일단 물체는 존재합니다(일반적으로). 이렇게 물체를 인식하는 메커니즘은 물체의 존재와는 독립적입니다. 일반적으로 성립하는 이 독립성 가정을 generic viewpoint assumption이라 합니다.

빛이 하나도 없는 공간에서 물체를 보면 어떨까요? 물체를 볼 수는 없지만 물체의 존재 자체가 바뀌진 않습니다. 물체, 조명 등이 물체를 인식하려는 우리의 움직임, 각도 등의 매커니즘과는 독립적으로 존재하며, 이러한 ‘불변성’으로부터 의자의 3차원 구조를 인지할 수 있는 것입니다.

그림 1. (원본 그림에서 좌우 그림만 바꾸었습니다.)

위 그림 1의 왼쪽 그림을 보면 의자인데요. 오른쪽 그림은 의자가 분리 되어 있습니다. 특정한 각도에서는 이 물체가 의자처럼 보이는데, 다른 각도에서 보면 사실은 완전한 의자가 아니었던(분리되어) 것입니다. 즉, 의자를 바라보는 각도(point of view)에 따라 달라보입니다. (이 의자를 Beuchet chair라고 한다네요.) 이 예시처럼 (일반적이지 않은) 특정한 각도에서는(accidental viewpoint) 위의 독립성 가정이 만족하지 않습니다. 이러한 아주 특별한 경우가 아니면, 위이 generic viewpoint assumption과 같은 메커니즘과 요소 간의 독립성 가정은 만족하게 됩니다.

The Principle of Independent Mechanisms

원인과 결과 문제(cause and effect problem)의 예제를 살펴봅시다(드디어!).

고도 A와 어떤 나라의 몇몇 도시들의 연간 평균 기온 T의 인과 관계를 알고 싶습니다. 어허.. 일단 우리의 상식을 빼고 생각해봅시다. 확률 모델과 데이터, 그리고 intervention 만으로 해본다고 해요.

두 개의 인과 모델이 있겠습니다.

1) 기온이 고도에 영향을 주는 모델: $T \longrightarrow A$

2) 고도가 기온에 영향을 주는 모델: $A \longrightarrow T$

이를 joint density function으로 표현하면, 각각 다음과 같이 표현(factorize)됩니다.

\[\begin{aligned} p(a,t)&=p(a|t)p(t) \qquad:T \longrightarrow A \\p(a,t)&=p(t|a)p(a) \qquad:A \longrightarrow T \end{aligned}\]

둘 간 인과관계를 알기 위해 intervention을 해봅시다. 그러니까, A 혹은 T에 의도적으로 값을 조작하는 것입니다.

먼저, 고도(A)를 높여봅시다. 즉, 한 도시의 땅을 의도적으로 높이는 것을 상상해봅시다. 그리고 실제로 기온이 낮아진 것을 관측했다고 해봅시다. 그리고 또 다른 intervention인 기온(T)를 높이는 것을 생각해봅시다. 한 도시에 엄청 큰 히팅 시스템을 두어서 도시 전체 온도를 높여보았더니, 고도가 낮아지진 않았다고 해봅시다. 즉, A를 바꾸면 T가 변하지만, T를 바꾸면 A가 변하진 않는다는 것을 확인했습니다. 따라서 이 두 번의 intervention으로부터 A는 T의 원인이라고 결론내릴 수 있습니다.

Intervenability

이제부터 매커니즘에 대해서 생각해봅시다. 고도가 바뀌었을 때, 평균 온도가 생성되는 어떤 물리적 메커니즘 $p(t \mid a)$ 이 있습니다. 이 물리적 메커니즘은 대기의 화학적 구성, 고도에 따라 압력이 감소하는 물리학, 바람의 기상 메커니즘 등을 포함합니다. 이 매커니즘은 유지되고, 온도는 변경된다고 가정해봅시다. 이는 도시들에 대한 분포 $p(a)$ 와는 독립적일 것입니다. 무슨 말이냐면, 예를 들어, 오스트리아와 스위스는 바로 옆에 있는 나라인데, 각 도시는 고도가 아주 약간 다를 순 있지만, 고도에 따라 온도가 바뀌는 물리적 메커니즘은 두 도시 모두에 동일하게 적용됩니다. 반대로 온도가 바뀌었을 때 고도에 대한 메커니즘 $p(a \mid t)$ 이 존재할지 생각해보면, 그렇지 않을 것입니다.

이렇게 되면, 서로 다른 도시의 고도와 온도의 결합 분포 $p(a,t)$ 가 주어지면 우리는 $p(a\mid t)p(t)$ 로 쓸 수는 있겠지만 $p(a\mid t)$ 가 invariant이므로 어떤 설명이 불가할 것입니다. 따라서 $p(t\mid a)p(a)$ 로 쓰는 것이 올바릅니다.

따라서, 여기서 얻을 수 있는 우리의 직관은 크게 두 가지가 됩니다:

1. A→T 가 올바른 인과 구조인 경우, 국소적인(localized) intervention을 수행할 수 있습니다. 즉, $p(t \mid a)$를 바꾸지 않고 $p(a)$ 를 바꿀 수 있습니다. 이는 위에서 말한 메커니즘이 독립이기 때문입니다.
2. $p(a)$와 $p(t\mid a)$는 autonomous, modular, or invariant 매커니즘 입니다.

여기선 가상의 intervention 실험으로 시작했지만, 실제 intervention이 없어도 인과 구조를 알아낼 수 있습니다. 다시 말해, 데이터 $p(a,t)$로부터 두 분해 방법 중 어떤 것이 autonomous, modular, or invariant 인지를 확인하여 인과 구조를 식별할 수 있다는 것입니다. 위의 예시를 다시 살펴보면, 오스트리아와 스위스의 고도와 기온의 결합 분포 $p^A(a,t)$, $p^S(a,t)$ 는 각 도시의 고도 $p^A(a)$, $p^S(a)$는 다르더라도 동일한 조건부 확률로 인과 인수분해할 수 있다는 것을 알 수 있습니다:

\[p^A(a,t)=p(t|a)p^A(a), p^S(a,t)=p(t|a)p^S(a).\]

Independence of information contained in mechanisms

위의 인과적 인수분해 $p(a,t)=p(t \mid a)p(a)$를 보면, 조건부 밀도 $p(t \mid a)$는 marginal 밀도 함수 $p(a)$에 대한 정보를 제공하지 않습니다. 이는 어떤 도시들에 intervention을 적용하든 해당 메커니즘은 영향을 받지 않음을 의미합니다. 반면에, $p(a,t) = p(a \mid t)p(t)$라면, 원인과 메커니즘의 독립성은 적용되지 않습니다.

Independence of noises

그래프 $A\rightarrow T$ 를 나타내는 SCM이 수반하는 분포를 다시 표현하면 다음과 같습니다.

\[\begin{aligned}A&:=N_A\\T&:=f_T(A,N_T)\end{aligned}\]

여기서 효과 T는 A의 노이즈(Noise) 함수로서 실현되며, $N_A$와 $N_T$는 통계적으로 독립인 노이즈 ($N_T \perp !!! \perp N_A$)입니다. $f_T$의 함수형태(functional form)에 적절한 제한을 가하면 두 가지 인과 구조($A\rightarrow T$ 또는 $T\rightarrow A$) 중 어느 것이 관찰된 $p(a,t)$를 수반하는지 식별할 수 있습니다(그러나 이러한 제한 없이 항상 두 가지 분해를 모두를 실현할 수 있습니다). 또한, 다변량인 경우 적절한 조건에서 공동 독립 노이즈를 가정하면 조건부 독립 테스트를 통해 인과 구조를 식별할 수 있습니다.

→ ANM과 같은 Functional Causal Discovery (Structure Identifiability) 방법을 참고하시면 됩니다!

이 모든 개념을 종합하여 정리하면 다음과 같습니다.

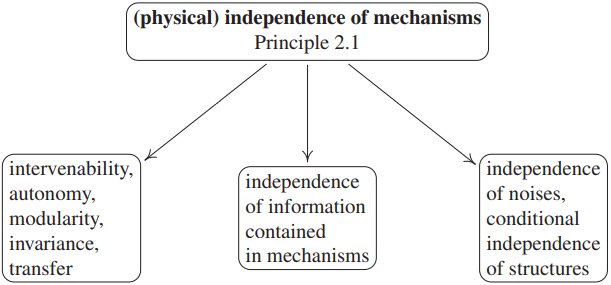
Principle 2.1 Independent mechanisms

The causal generative process of a system’s variables is composed of autonomous modules that do not inform or influence each other. In the probabilistic case, this means that the conditional distribution of each variable given its causes (i.e. its mechanism) does not inform or influence the other conditional distributions. In case we have only two variables, this reduces to an independence between the cause distribution and the mechanism producing the effect distribution.

1. 메커니즘 독립성의 물리적 측면. 다른 메커니즘에 영향을 주지 않고 하나의 메커니즘을 변경할 수 있음을 의미합니다. 즉, 한 메커니즘에 intervention을 해도 다른 메커니즘에는 불변(invariant)입니다.
2. 메커니즘 독립성의 정보이론적 측면. 물리적으로 결합된 메커니즘은 통계적/알고리즘적 정보 측정 측면에서 정량화될 수 있는 정보를 생성합니다. 효과에는 원인에 대한 정보가 포함되어 있지만, Independent Principle에 따라 원인에서 효과를 생성하는 메커니즘에는 원인을 생성하는 메커니즘에 대한 정보가 포함되어 있지 않습니다. 2개 이상의 노드가 있는 인과 구조의 경우 독립 원칙은 직접적인 원인으로부터 모든 노드를 생성하는 메커니즘에 서로에 대한 정보가 포함되어 있지 않다는 것을 나타냅니다.
3. 메커니즘 독립성과 노이즈 독립성의 관계. SEM(구조방정식 모델링)에서 일반적으로 사용되는 노이즈 독립성 가정과 연관이 있습니다. 노이즈 N이 이산형 변수가 $s$로 고정될 때, 할당 $E:=f(C,N)$은 $E:=f^s(C)$가 됩니다. 즉, 노이즈가 수많은 $f^s$를 결정하게 됩니다. 그리고 변수 $X_j,X_k$의 두 메커니즘에 대한 노이즈 변수가 통계적으로 종속이라고 가정하면, 노드 j와 k에 대한 정보를 알게 되어, 이는 independent principle에 위배됩니다. 다음 단원(3.)에 나오겠지만, Additive Noise $E:=f(C)+N$는 노이즈 값에 따라서 메커니즘은 바뀌지 않으면서 효과가 오직 shift되므로 independent principle에 위배되지 않습니다.

이 원리는 인과 구조에 대한 정보를 제공할 수 있으며, 가정에 따라 다를 수는 있습니다. 그리고 중요한 것은, 모든 시스템이 이 원칙을 충족할 수는 없습니다.