Federated Learning 이란?

이 글은 연합학습(Federated Learning)에 대한 개념과 문제를 소개하고, 이를 해결하기 위한 몇 가지 방법을 소개합니다. 연구 분야에 대해서 소개할 기회들이 몇몇 있었는데 그때마다 만들었던 자료들을 모아서 작성하였습니다. (그래서 영어와 한글이 아직 혼용되어 있어요..)

What is Federated Learning?

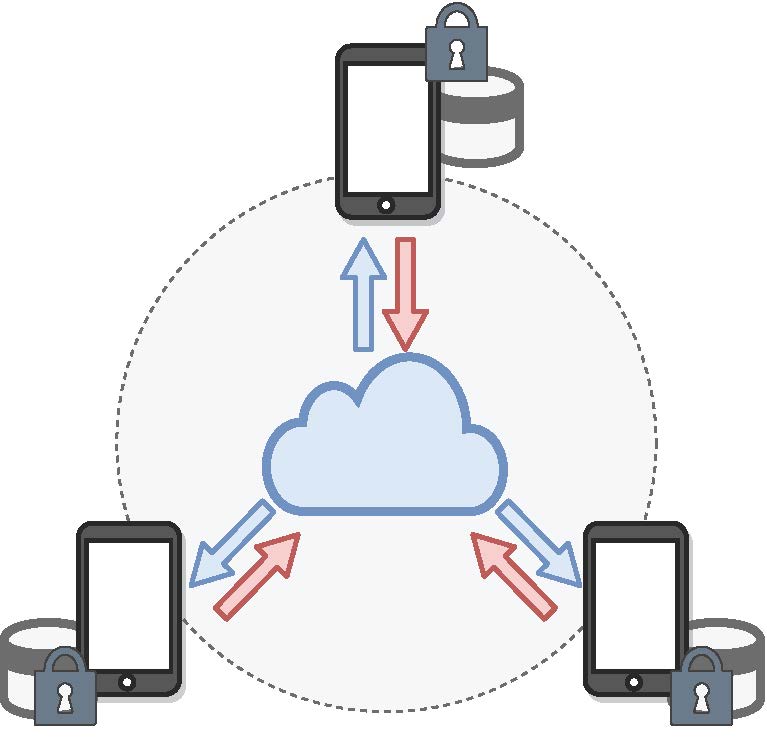
Federated Learning (연합학습)은 하나의 중앙 server와 여러 개의 분산된 client가 존재할 때 여러 client가 ‘연합’하여 각자 학습한 후 하나의 모델을 만드는 문제입니다. 여기서, 일반적인 distributed learning과 다른 점은 Federated Learning은 각 client의 data의 privacy를 중요하게 여겨, 해당 데이터는 각 client 내부적으로만 가지고 있고, 다른 client와 교환하거나 중앙 서버로 보낼 수 없다고 가정합니다. 따라서 데이터가 유출되어서도, 복원되어서도 안됩니다. 각 클라이언트는 데이터를 보내지 않고 ‘모델 학습 정보’만을 중앙 서버로 보냅니다. 그리고 서버에서는 각 클라이언트로부터 해당 정보를 받아 합친 후 업데이트하여 다시 각 클라이언트로 보내게 됩니다. 이를 통해 각 클라이언트의 privacy를 보호할 수 있고, 중앙 서버에서는 데이터를 모을 storage를 구비할 필요가 없으며 모델 학습을 위한 하드웨어 리소스도 효율적으로 사용할 수 있습니다. 최근 구글, 애플 등에서 연구되고 서비스에 적용되고 있는 분야입니다.

Fig 1. 연합학습 예시 그림

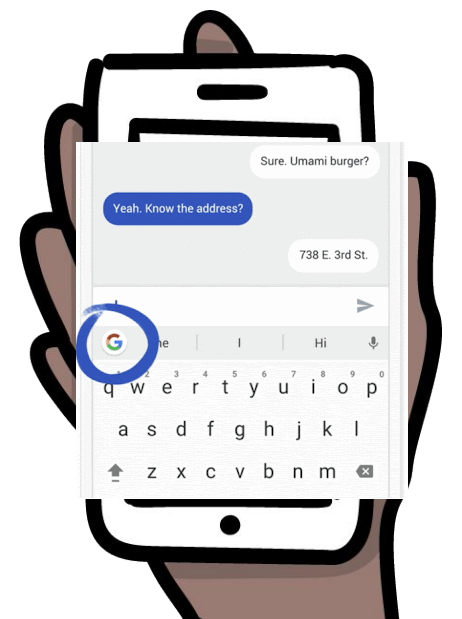
Fig 2. Google Gboard 연합학습 예시 (source: link)

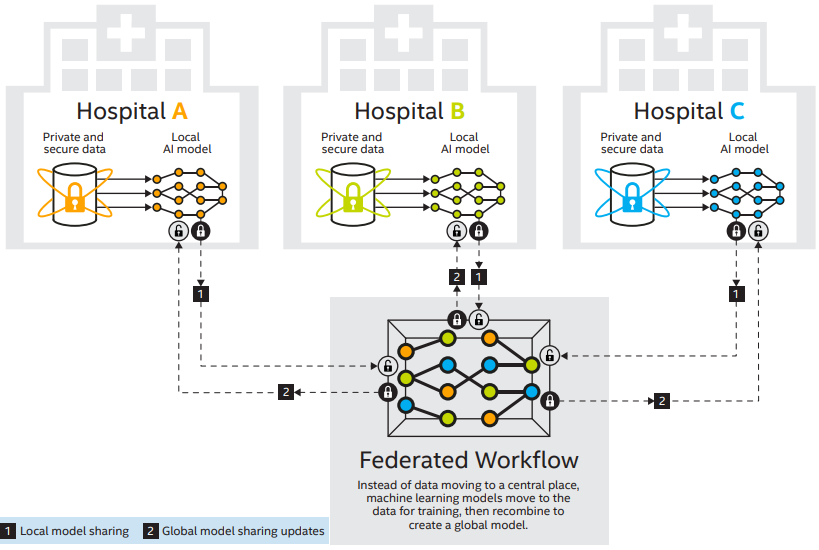
Fig 3. 병원 협력 연합학습 예시 (source: link)

Problem Statement

Federated Learning에서는 communication(서버와 클라이언트 간 정보 전송)을 효율적으로 적게 하는 것(communication-efficient)이 privacy-preserving과 함께 중요한 목표입니다. 정보를 최대한 적게 주고 받음으로써 정보 전송 시 발생하는 cost를 최대한 줄이면서도 좋은 모델을 만들어야 합니다.

Challenges

연합학습은 그 실용성 때문에 굉장히 현실적인 상황들을 가정합니다. 먼저, 학습에 참여하는 클라이언트들은 굉장히 많거나 (cross-device setting), 각자의 집단적 특징들이 다를 수 있기 때문에 (cross-silo setting), 클라이언트 간 데이터의 특성이 다를 수 있습니다. 즉, 데이터가 같은 분포로부터 독립적으로 생성되었다는 I.I.D. 가정을 파괴합니다. 이 가정은 일반적인 머신러닝에서 굉장히 중요하며 일반적으로 만족함을 가정하므로 이 가정이 파괴된 상황에선 이를 잘 고려하고 머신러닝 연합학습 모델을 만들어야 합니다. 이를 statistical heterogeneity라고 합니다.

또 다른 현실적인 가정은 각 클라이언트가 가진 하드웨어, 소프트웨어, 네트워크 등이 모두 달라 발생할 수 있는 문제점을 말합니다. 클라이언트들이 학습에 참여하기 위해 중앙 서버의 네트워크에 연결하고자 하면, 네트워크 bandwidth의 한계로 모든 클라이언트들이 참여하지 못할 수 있습니다. 혹은 인터넷 연결 상황이 좋지 않아 비동시적 (asynchronous)인 학습을 해야하거나, 각 클라이언트가 가진 학습 리소스가 달라 학습 성능이 서로 굉장히 다를 수 있습니다. 이를 system heterogeneity라고 합니다.

Problem Formulation

Global Objective (Server-side)

\[\begin{align} \min_{\mathbf{w}} F(\mathbf{w})=\min_{\mathbf{w}}\left[\sum_{k=1}^Kp_kF_k(\mathbf{w}) \right], \end{align}\]

where \(F(\cdot)\) is the global objective function and \(F_k(\cdot)\) is a local objective function of client \(k\), which indicates the client index, \(k \in [K]\). \(p_k\) is the value that satisfies \(\sum_{k=1}^Kp_k=1\). In general, we use the ratio of the number of data points of each client: \(p_k=n_k/\sum_{k=1}^Kn_k\) where \(n_k\) is the number of local data points of the dataset of \(k\)-th client \(\mathcal{D}_k\), $n_k:=\mid \mathcal{D}k\mid$.

Local Objective (Client-side)

\[\begin{align} \min_{\mathbf{w}} F_k(\mathbf{w})=\min_{\mathbf{w}}\frac{1}{n_k}\sum_{\xi\in\mathcal{D}_k}f(\mathbf{w},\xi), \end{align}\]

where $f(\cdot,\xi)$ denotes loss function for sample $\xi$.

FedAvg: a common algorithm of federated learning

FedAvg [1] is a pioneering work, regarding as distributed SGD while preserving privacy. It assume that the server can only accept a fraction of the total clients to participate in the current training at each communication round. We denote $\mathcal{S}_t$ as the subset of these selected clients active clients at the current round $t$ and its size is $S$, which indicates only maximum $S$ clients participate in the current round.

Global Update (Server-side)

Each selected client gets the current global model:

\[\begin{align} \mathbf{w}_k^{(t)}\leftarrow \mathbf{w}^{(t)}, \end{align}\]

where $\mathbf{w}_k^{(t)},\mathbf{w}^{(t)}$ mean the local model of client $k$ and the global model at round $t$ respectively.

Local Update (Client-side)

Each client train the model with their local data:

\[\begin{align} \mathbf{w}_k^{(t,i+1)}\leftarrow \mathbf{w}_k^{(t,i)}-\eta_l \cdot g_k(\mathbf{w}_k^{(t,i)}), \end{align}\]

where $\mathbf{w}_k^{(t,i)}$ denotes a local model of client $k$ at $i$-th local SGD update of round $t$. $g_k(\mathbf{w}_k^{(t)}):=\nabla f_k(\mathbf{w},\xi)$ is the gradient of $f_k(\mathbf{w})$ with respect to $\mathbf{w}$. $\eta_l$ is the local learning rate for local training. $i$ denotes an index number of local SGD updates that satisfies $i \in (0,\tau]$ where $\tau$ indicates a maximum number of local SGD updates. If the number of local training epoch $E$ is 1 and $B$ indicates the mini-batch size for local training, $\tau=[n_k/B]+1$. The device of the client performs local SGD updates up to $\tau$ iterations with their local data at the current round and sends their updated local model to the server.

Aggregation (Server-side)

The server gets the updated local models from each client and it aggregates them as:

\[\begin{align} \mathbf{w}^{(t+1)}\leftarrow \mathbf{w}^{(t)}-\eta_g\cdot \frac{1}{S} \sum_{k\in \mathcal{S}_t} (\mathbf{w}_k^{(t,\tau)}-\mathbf{w}^{(t)}), \end{align}\]

where $\eta_g$ is global learning rate. FedAvg uses $\eta_g$ as 1. This aggregation scheme induces:

\[\mathbf{w}^{(t+1)}=\frac{1}{m}\sum_{k\in \mathcal{S}_t} \mathbf{w}_k^{(t)}.\]

Global Objective (Server-side)

The final objective of FedAvg can be rewritten as follows:

\[\begin{align} F(\mathbf{w}^{(t+1)})=\sum_{k\in \mathcal{S}_t}p_kF_k(\mathbf{w}_k^{(t,\tau)}). \end{align}\]

Related Works

Many existing works have approached this problem by changing the model aggregation algorithm in federated learning such as FedOpt [2].

Benchmark datasets

We evaluated client selection methods for federated learning in various practical experimental settings. We used three common databases for federated learning: EMNIST, CelebA, CIFAR10 for image classification. They are partitioned across clients by various methods.

FedEMNIST

Federated EMNIST dataset that we use is the modified extensive MNIST dataset [4] as partitioning for federated learning based on FedOpt, which is built upon benchmark work, LEAF [3]. The dataset is partitioned by human writing in a natural way as FedOpt, which means the dataset is distributed as heterogeneous. FedEMNIST dataset is constructed with 3,400 clients for training and the same number of clients for the test (but, it depends on the experimental settings).

FedCelebA

We used CelebA dataset [5] partitioned for federated learning setting according to LEAF. The data of CelebA is distributed to 9,343 clients for both train and test set, that is partitioned by each identifier (person). Thus, FedCelebA dataset is heterogeneous across clients with respect to the number of local data.

FedCIFAR10

Following [6], CIFAR10 dataset can be partitioned into each client using Dirichlet distribution. The criteria of allocation depend on the hyperparameter ($\alpha_D$), which indicates the partitioning rate. It samples the number of distributed samples with respect to classes from Dirichlet distribution and partitions data to each client. That makes decentralized dataset imbalance in terms of the number of local data points as well as labels.

Reference

[1] B. McMahan, E. Moore, D. Ramage, S. Hampson, and B. A. y. Arcas, “Communication-Efficient Learning of Deep Networks from Decentralized Data,” in Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, vol. 54. PMLR, 2017, pp. 1273–1282.

[2] S. J. Reddi, Z. Charles, M. Zaheer, Z. Garrett, K. Rush, J. Koneˇcný, S. Kumar, and H. B. McMahan, “Adaptive federated optimization,” in International Conference on Learning Representations (ICLR), 2021.

[3] S. Caldas, S. M. K. Duddu, P.Wu, T. Li, J. Koneˇcný, H. B. McMahan, V. Smith, and A. Talwalkar, “Leaf: A benchmark for federated settings,” in NeurIPS Workshop on Federated Learning for Data Privacy and Confidentiality, 2019.

[4] G. Cohen, S. Afshar, J. Tapson, and A. van Schaik, “Emnist: an extension of mnist to handwritten letters.” in 2017 International Joint Conference on Neural Networks (IJCNN), 2017.

[5] Z. Liu, P. Luo, X. Wang, and X. Tang, “Deep learning face attributes in the wild,” in Proceedings of the IEEE International Conference on Computer Vision (ICCV), 2015.

[6] Y. Fraboni, R. Vidal, L. Kameni, and M. Lorenzi, “Clustered sampling: Low-variance and improved representativity for clients selection in federated learning,” in Proceedings of the 38th International Conference on Machine Learning (ICML), vol. 139. PMLR, 2021, pp. 3407–3416.

[7] P. Kairouz, H. B. McMahan, B. Avent, A. Bellet, M. Bennis, A. N. Bhagoji, K. Bonawitz, Z. Charles, G. Cormode, R. Cummings, R. G. L. D’Oliveira, H. Eichner, S. E. Rouayheb, D. Evans, J. Gardner, Z. Garrett, A. Gascón, B. Ghazi, P. B. Gibbons, M. Gruteser, Z. Harchaoui, C. He, L. He, Z. Huo, B. Hutchinson, J. Hsu, M. Jaggi, T. Javidi, G. Joshi, M. Khodak, J. Konecný, A. Korolova, F. Koushanfar, S. Koyejo, T. Lepoint, Y. Liu, P. Mittal, M. Mohri, R. Nock, A. Özgür, R. Pagh, H. Qi, D. Ramage, R. Raskar, M. Raykova, D. Song, W. Song, S. U. Stich, Z. Sun, A. T. Suresh, F. Tramèr, P. Vepakomma, J. Wang, L. Xiong, Z. Xu, Q. Yang, F. X. Yu, H. Yu, and S. Zhao, “Advances and open problems in federated learning,” Foundations and Trends® in Machine Learning, vol. 14, no. 1–2, pp. 1–210, 2021.