Introduction to Multi-Task Learning

이 글에서는 Multi-Task Learning이란 무엇이고, 어떤 장점을 가지며 Classical 하게 어떤 방법들을 가지고 있는지 소개하고자 합니다. 다음 글에서는 Deep Learning에서 MTL 방법들을 소개하겠습니다.

전체적으로 글의 흐름은 하나의 큰 물음에 대해 MTL이 어떻게 설명하고, 해결하는지를 설명하면서 진행합니다.

1. Introduction to Multi-Task Learning

이번 섹션에서는 MTL이 무엇인지, MTL은 어떤 장점을 가지고 있는지에 대한 내용을 설명합니다. 이를 위해 MTL을 거의 처음으로 소개한 논문인 R. Caruana의 Multitask learning[1] 을 인용하며 설명하고자 합니다.

Multi-Task Learning이란?

Multi-Task Learning은 서로 다른 task들을 예측할 때, task 모두 혹은 일부가 어떤 knowledge를 공유한다고 가정하고 이를 고려해 한 모델 안에 함께 학습하여 더 좋은 예측 성능을 내는 모델을 말합니다. MTL은 task들이 학습할 때 각 task의 정보가 서로의 학습에 도움이 되어 성능을 높일 수 있다는 가정을 가집니다. 따라서, MTL은 학습 시간 및 추론 시간을 줄이면서 함께 학습함으로써 예측 성능을 높일 수 있으며 shared representation을 잘 학습할 수 있습니다.

어떻게 MTL은 일반화 성능을 높일 수 있을까?

MTL을 거의 처음으로 소개한 논문인 [1]에서는 다음과 같이 말합니다: backprop에서 추가적인 output을 더하면, 이것이 서로 관련이 없는 task들 사이에서는 noise로써 작동하거나 weight 업데이트를 dynamic하게 하거나, net capacity를 줄여준다고 언급합니다. 다시 말하면, 한 task에 대해서 uncorrelated task는 noise로 학습하면서 더 일반화 성능이 높아지고, correlated task의 경우, 이 task의 학습이 weight에 고려되어 함께 업데이트 될 수 있습니다. (net capacity를 줄여주는 것은 각 task에 대해 network를 학습하는 것보다는 capacity를 줄여준다고 생각했습니다만 확실하지 않습니다.)

또한, [1]논문에서 말하는 MTL의 4가지 매커니즘에 대해 간단하게 소개하고자 합니다. 먼저, Statistical Data Amplification은 한 task의 학습에 관련해 다른 task의 학습은 하나의 data 증폭이라고 여길 수 있습니다. 즉 함께 학습함으로써 task 관점에서 각자의 데이터 뿐만 아니라 서로의 데이터를 더 많이 이용할 수 있다는 관점입니다. 둘째, Attribute Selection입니다. task들을 학습하는 과정에서 어떤 task가 도움이 되는지, 더 관련되어 있는지 선택하는 과정이 attribute selection이라고 할 수 있습니다. 셋째, 엿듣기라는 뜻을 가진 eavesdropping은 task 학습 시 다른 task들이 학습하는 히든 레이어를 ‘엿듣게’ 될 수 있습니다. 마지막으로, Representation Bias는 MTL은 다른 태스크들이 선호하는 hidden layer representation을 선호한다는 bias를 가진다. MTL의 inductive bias 차원을 말한 것 같습니다.

2. Classical methods of MTL

Multi-Task Learning에는 다양한 방법 및 적용이 있습니다. 이번 챕터에서는 Deep Neural Network 이전의 방법들에 대해 논하고자 합니다.

1. Regularized Multi-Task Learning

MTL에서 sharing knowledge를 어떻게 표현하고, 어떻게 학습할 수 있을까?

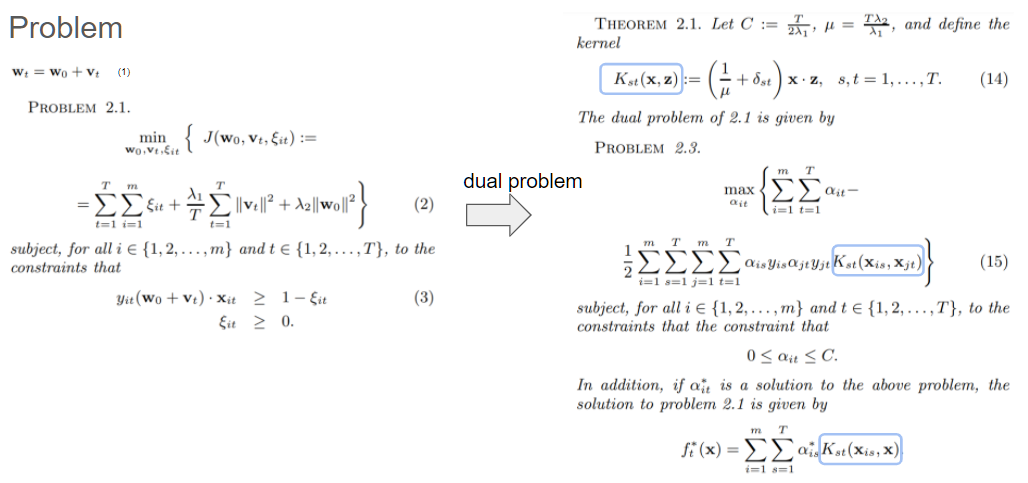
이 논문[2] 에서는 sharing knowledge를 kernel function의 parameter를 이용하고, optimization에 regularization term을 추가합니다. 이는 Regularization을 사용하는 첫 논문이라고 할 수 있습니다. 커널 함수 정의 시, task coupling parameter를 두고, 이것이 task 간의 어떤 knowledge를 공유할 수 있는 정도를 나타낼 수 있도록 정의합니다. 이 파라미터가 작다, 즉 task 간 공유할 수 있는 여지가 적다면, single task learning과 같은 역할을 할 수도 있게 됩니다. 여기서 커널은 어떤 커널도 사용할 수 있습니다(아마 positive-definite kernel이겠죠). 그리고, Regularization을 사용해 task 간 관련성을 적절하게 나누고 학습할 수 있는 역할을 합니다. 여기서 regularization을 loss function에 추가시키고, 이를 커널을 이용해 dual problem으로 바꿉니다. 이를 통해 우리는 MTL이 쉽게 optimize될 수 있도록 합니다.

다만, 모든 task들이 관련있다는 가정을 하고, 모든 task들이 관련이 없어 아예 고려하지 않는 경우를 생각하지 않습니다.

Regularized Multi-Task Learning

2. (Convex) Multi-Task Feature Learning

MTL에서 어떤 task가 관련이 있는가?

이 논문[3] 에서는 MTL의 고전적 가정인 모든 task가 서로 관련이 있다를 회피하고 관련이 있는 일부 task만 골라 학습하는 방법을 소개합니다. 여기서는 task에 대한 representation을 low-dimension으로 바꿔 학습합니다. 한 태스크를 학습하는 데에 관련이 있는 태스크는 일부라고 가정하고, 저차원에서 관련이 있는 task들만 남기고 학습할 수 있게 됩니다.

구체적으로, task parameter에 대한 matrix를 low rank로 factorize하여 관련이 있는 task들만 남길 여지를 만들고, optimization 단계에서 regularization term을 $l_{2,1}$ norm으로 바꿔, 실제로 parameter를 share할 task들만 남길 수 있도록 합니다. 몇 개의 task들만 parameter, 즉 knowledge를 share할지는 regularization parameter를 통해 조절될 것입니다. 이렇게 하면 task들에 대해 공통으로 몇 개의 feature들만 학습할 수 있게 됩니다.

다만, 관련이 있냐 없냐만 볼 수 있고 관련이 없는 애들끼리의 관계를 볼 수 없습니다.

Multi-Task Feature Learning

3. Learning with Whom to Share in Multi-task Feature Learning

Negative Transfer, 즉 같이 학습하면 오히려 더 성능이 나빠지는 unrelated tasks가 있다면?

이 논문[4] 에서는 MTL의 고전적 문제인 Negative Transfer을 task group을 둠으로써 해결합니다. MTL에서 전체 혹은 일부가 관련이 있었다면, 여기서는 task group 내에서는 서로 관련이 있고 서로 다른 group끼리는 함께 학습하지 않는 방법을 소개합니다.

위의 MTFL 논문처럼, task matrix를 low-dimensional representation을 위해 factorization하고 거기에 관련 있는 task group에 대한 index matrix로 한 번 더 factorize합니다. 그리고 이 matrix에 대한 regularization term을 통해 어떤 task group인지, 그 안에서는 어떤 task들이 관련 있는지에 대한 matrix 형태로 나타낼 수 있습니다.

또한, 이 논문에서는 class간 유사도가 성공적인 task knowledge sharing으로 이어지지 않음을 보여줍니다.

단, negative하게 강한 관련성이 있는 task들을 잘 선별하지 못할 수 있습니다.

**

4. Multi-Task Gaussian Process Prediction

Negative Transfer를 GP를 이용해서는 어떻게 해결하는가?

이 논문[5] 에서는 GP에서의 MTL을 다루고 있습니다. GP에서 task descriptor를 정의하기 위해 task들끼리의 covariance function을 share함으로써 inter-task dependency를 사용합니다.

커널함수의 inner-product를 task-similarity matrix와 covariance function으로 나눕니다. task-similarity matrix는 예로, task들이 cluster 형태가 되면 block diagonal matrix 형태를 가지게 됩니다.

(..ing)

Reference

[1] Caruana, R. (1997). Multitask learning. Machine learning, 28(1), 41-75.

[2] Evgeniou, T., & Pontil, M. (2004, August). Regularized multi–task learning. In Proceedings of the tenth ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 109-117).

[3] Argyriou, A., Evgeniou, T., & Pontil, M. (2006). Multi-task feature learning. Advances in neural information processing systems, 19, 41-48.

[4] Kang, Z., Grauman, K., & Sha, F. (2011, June). Learning with Whom to Share in Multi-task Feature Learning. In ICML (Vol. 2, No. 3, p. 4).

[5] Bonilla, E. V., Chai, K., & Williams, C. (2007). Multi-task Gaussian process prediction. Advances in neural information processing systems, 20, 153-160.