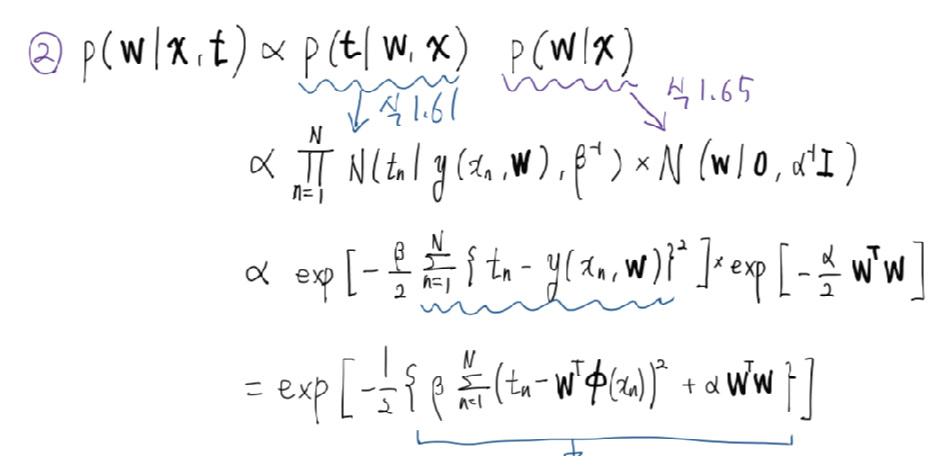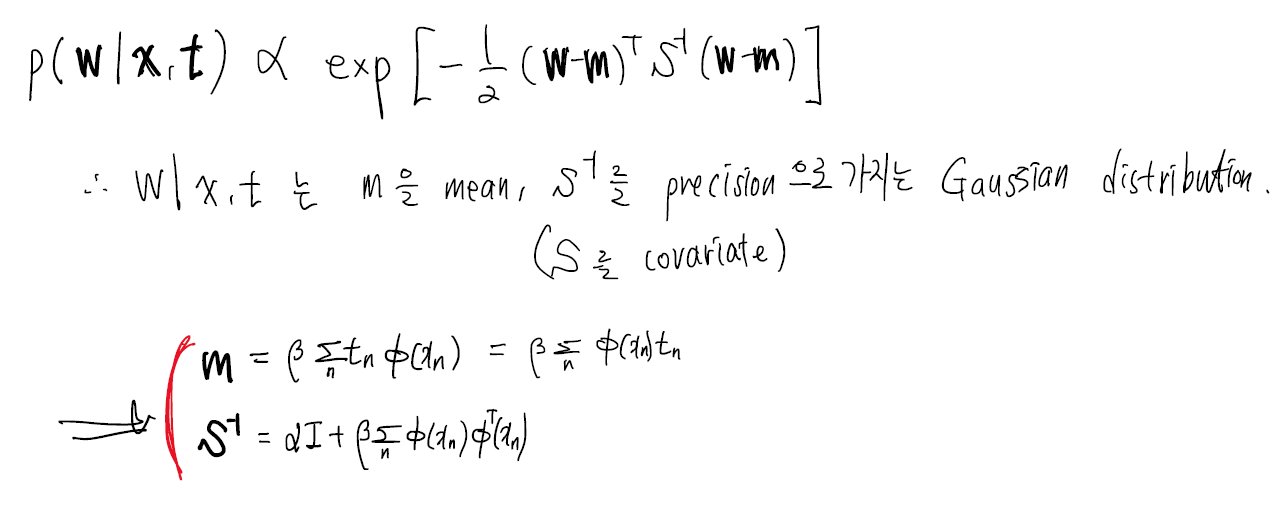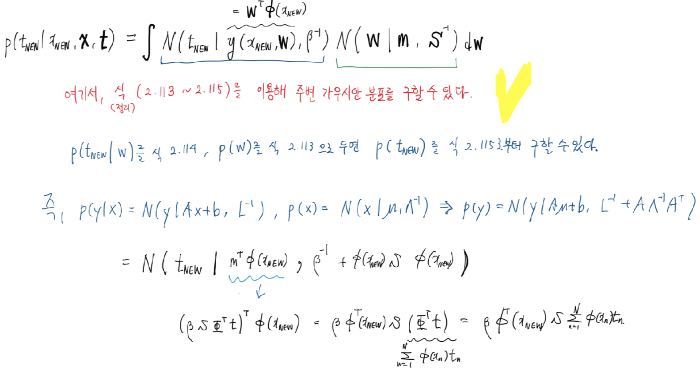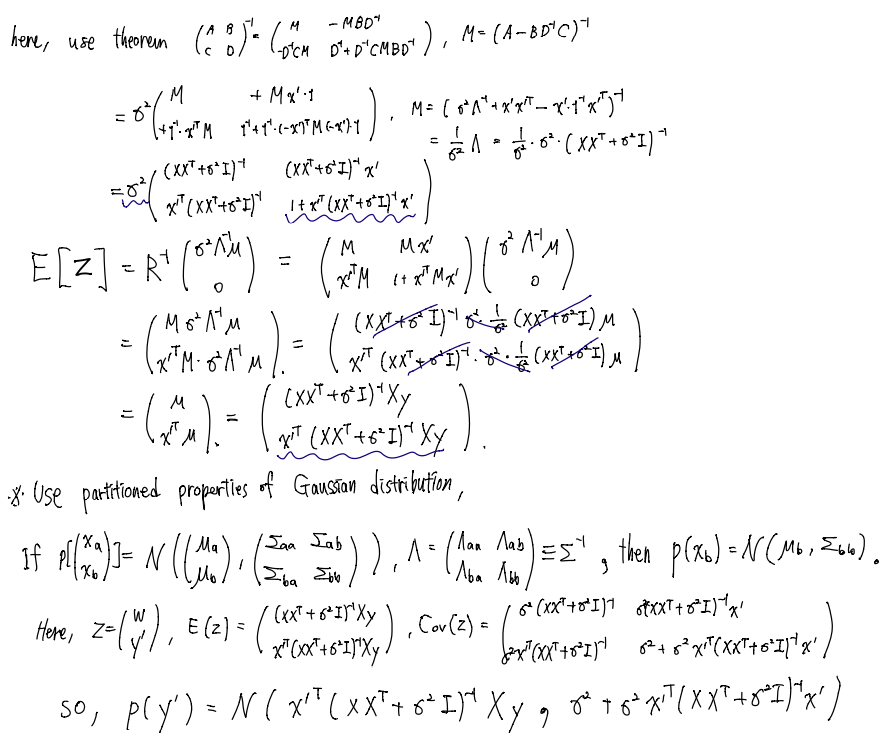Bayesian Linear Regression

Posted Dec 6, 2020

By 6 min read

먼저, 이 글은 PRML (CH3) 공부를 바탕으로 작성된 글입니다. 따라서, 간혹 틀리다거나 더 좋은 해석이 있다면 편하게 댓글 부탁드립니다!

이 글에서는 우리가 흔히 알고 있는 Linear Regression에 Bayesian Approach를 적용하는 Bayesian Linear Regression에 대해 다룹니다.

Linear Regression

먼저, Linear Regression에 basis function을 이용하면, Linear에서 벗어난 형태를 나타낼 수 있습니다.

\[y(\mathbf{x},\mathbf{w})=w_0+\sum_{j=1}^{M-1}w_j\phi_j(x)=\mathbf{w}^T\phi(\mathbf{x})\]

우리는 이러한 Linear Regression에 MLE(Maximum Likelihood Estimation) 방법을 이용해 parameter를 추정(estimation)합니다.

여기에 Bayesian Approach를 이용하면 MLE에서 발생할 수 있는 overfitting 문제를 피하고 training data만으로 model complexity를 결정할 수 있습니다. 이에 대해 자세히 살펴보겠습니다.

Parameter distribution

먼저, 데이터에 대한 가능도(likelihood) 함수를 정의합니다. 이때, 데이터의 noise가 Gaussian distribution을 따른다고 가정하므로 likelihood는 다음과 같이 쓸 수 있습니다. 여기서 noise의 variance인 \(\beta\)는 알고 있는 상수값(known constant)라고 가정합니다.

\[p(\mathbf{t}|\mathbf{X},\mathbf{w},\beta)=\prod_{n=1}^{N}\mathcal{N}(t_n|\mathbf{w}^T\phi(\mathbf{w}_n,\beta^{-1})\]

Bayesian 방법을 사용하므로 우리는 parameter의 distribution, 즉 prior가 필요합니다. 여기서는 likelihood를 Gaussian으로 사용하므로 계산의 편리성을 위해 parameter의 distribution을 Gaussian의 conjugate distribution인 같은 Gaussian distribution으로 가정합니다.

\[p(\mathbf{w})=\mathcal{N}(\mathbf{w}|\mathbf{m}_0,\mathbf{S}_0)\]

이렇게 정의하면, 우리는 Bayesian Rule에 의해 posterior를 다음과 같이 유도할 수 있습니다.

\[p(\mathbf{w}|\mathbf{t})=\mathcal{N}(\mathbf{w}|\mathbf{m}_N,\mathbf{S}_N)\] \[\mathbf{m}_N=\mathbf{S}_N(\mathbf{S}_0^{-1}\mathbf{m}_0+\beta\boldsymbol{\Phi}^T\mathbf{t})\] \[\mathbf{S}_N^{-1}=\mathbf{S}_0^{-1}+\beta\boldsymbol{\Phi}^T\boldsymbol{\Phi}\]

여기서, posterior의 maximum을 구하는 MAP(Maximum A Posterior)의 값은 Gaussian 분포의 특성에 따라 평균이 됩니다. 즉, \(\mathbf{w}_{MAP}=\mathbf{m}_N\). 또한, Bayesian 방법의 특성이라고 할 수 있는, 데이터가 없는 경우(\(N=0\)), prior는 posterior와 같게 되고, \(\mathbf{S}_0=\alpha^{-1}\mathbf{I}\)에서 \(\alpha \longrightarrow 0\)인 경우엔 MAP는 MLE와 같게 됩니다.

[Proof] 이를 증명해봅시다.

증명의 편의를 위해, prior를 0을 평균으로 가지고 \(\alpha\)를 가지는 Gaussian distribution으로 정의합니다. 즉, \(\mathbf{m}_0=0\), \(\mathbf{S}_0=\alpha^{-1}\mathbf{I}\) 이며 다음과 같이 표현됩니다.

\[p(\mathbf{w}|\alpha) = \mathcal{N}(0, \alpha^{-1}\mathbf{I})\]

이에 따라 posterior는 아래와 같습니다.

\[\mathcal{N}(\mathbf{w}|\mathbf{m}_N,\mathbf{S}_N)\] \[\mathbf{m}_N=\beta\mathbf{S}_N\boldsymbol{\Phi}^T\mathbf{t}\] \[\mathbf{S}_N^{-1}=\alpha\mathbf{I}+\beta\boldsymbol{\Phi}^T\boldsymbol{\Phi}\]

여기서, 안쪽 exp 수식을 보면,

로 나타낼 수 있습니다. 그리고, 다시 exp 안으로 넣으면 비례식 형태로 확률분포를 보일 수 있습니다. 따라서,

로써 증명될 수 있습니다.

log posterior는 아래와 같이 log likelihood + log prior로 나타낼 수 있습니다.

\(\mathrm{ln}p(\mathbf{w}|\mathbf{t})=-\frac{\beta}{2}\sum_{n=1}^N\{t_n-\mathbf{w}^T\phi(\mathbf{x}_n)\}^2-\frac{\alpha}{2}\mathbf{w}^T\mathbf{w}+const\) 이 posterior를 \(\mathbf{w}\) 에 대해 최대화하는 것은 squared regularized term을 포함한 squared error function을 최소화하는 것과 같습니다. (\(\lambda=\alpha/\beta\))

Predictive distribution

이제, 위에서 적합(fit)한 회귀모델을 이용해 예측을 하고자 합니다.

예측분포(predictive distribution)를 만들기 위해 여기서는 새로운 \(\mathbf{x}\) 값에 대하여 \(t\)의 값을 예측하는 경우를 고려합니다.

\[\int p(t|\mathbf{t},\alpha,\beta)=\int p(t|\mathbf{w},\beta) p(\mathbf{w}|\mathbf{t},\alpha,\beta) d\mathbf{w}\]

로부터 다음을 구할 수 있게 됩니다.

\[p(t|\mathbf{x},\mathbf{t},\alpha,\beta)=\mathcal{N}(t|\mathbf{m}_N^T \phi(\mathbf{x}), \sigma_N^2(\mathbf{x}))\] \[\sigma_N^2(\mathbf{x})=\beta^{-1}+\phi(\mathbf{x})^T\mathbf{S}_N\phi(\mathbf{x})\]

[Proof] 이를 증명해봅시다.

증명의 편의를 위해, 위에서처럼 prior를 0을 평균으로 가지고 \(\alpha\)를 가지는 Gaussian distribution으로 정의합니다. 또한, 위에서 다음과 같은 likelihood와 prior를 가정하였습니다.

\[p(t|\mathbf{x},\mathbf{w},\beta)=\mathcal{N}(t|y(\mathbf{x},\mathbf{w}),\beta^{-1})\] \[p(\mathbf{w}|\mathbf{t})=\mathcal{N}(\mathbf{w}|\mathbf{m}_N,\mathbf{S}_N)\]

이를 잘 기억하고, 증명을 하고자 합니다. 이 글에서는 marginal Gaussian의 theorem을 이용해 증명하겠습니다. 그 정리만을 이용하면 한 줄로 끝날 수 있지만, 이에 대한 증명을 포함해 더 자세하게 증명을 하겠습니다. 그 정리는, PRML 책을 인용하면,